
���� ��1��Բ�ĵ�ֱ��x-y+$\sqrt{2}$=0�ľ���d=$\frac{|0-0+\sqrt{2}|}{\sqrt{1+1}}$=1���Ӷ�ȷ��b=1���Ӷ��̣�
��2����ֱ��MN�ķ���Ϊx-1=ay���Ӷ��������̻���ã�a2+2��y2+2ay-1=0���Ӷ��ɵ�y1+y2=-$\frac{2a}{{a}^{2}+2}$��y1y2=-$\frac{1}{{a}^{2}+2}$���Ӷ������|y1-y2|max=$\sqrt{2}$���Ӷ�����������ֵ��
��� 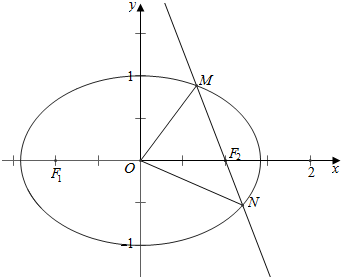 �⣺��1��Բ�ĵ�ֱ��x-y+$\sqrt{2}$=0�ľ���d=$\frac{|0-0+\sqrt{2}|}{\sqrt{1+1}}$=1��
�⣺��1��Բ�ĵ�ֱ��x-y+$\sqrt{2}$=0�ľ���d=$\frac{|0-0+\sqrt{2}|}{\sqrt{1+1}}$=1��
��b=1��
�֡�e=$\frac{\sqrt{2}}{2}$��
��c=1��a=$\sqrt{2}$��
����ԲC�ı�����Ϊ$\frac{{x}^{2}}{2}$+y2=1��
��2����ֱ��MN�ķ���Ϊx-1=ay��
�������̿ɵ�$\left\{\begin{array}{l}{x=1+ay}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$��
��a2+2��y2+2ay-1=0��
��M��x1��y1����N��x2��y2����
��y1+y2=-$\frac{2a}{{a}^{2}+2}$��y1y2=-$\frac{1}{{a}^{2}+2}$��
�ʣ�y1-y2��2=��y1+y2��2-4y1y2
=$\frac{4{a}^{2}}{��{a}^{2}+2��^{2}}$+4$\frac{1}{{a}^{2}+2}$
=$\frac{8{a}^{2}+8}{��{a}^{2}+2��^{2}}$=8��-$\frac{1}{��{a}^{2}+2��^{2}}$+$\frac{1}{{a}^{2}+2}$��
=-8��$\frac{1}{{a}^{2}+2}$-$\frac{1}{2}$��2+2��
��|y1-y2|max=$\sqrt{2}$��
��S=$\frac{1}{2}$|OF2|��|y1|+|y2|��
=$\frac{1}{2}$|OF2||y1-y2|
��$\frac{1}{2}$•1•$\sqrt{2}$=$\frac{\sqrt{2}}{2}$��
�ʡ�0MN���S�����ֵΪ$\frac{\sqrt{2}}{2}$��
���� ���⿼�������ν�ϵ�˼��Ӧ�ü���Բ��ֱ�ߵ�λ�ù�ϵӦ�ã�ͬʱ������ѧ���Ļ�������������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
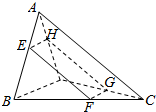 �ռ��ı���ABCD����������AC��BD���ഹֱ��AC��BD�ij��ֱ�Ϊ8��2����ƽ���ı�����������Ľ����ı���EFGH��ƽ�ƹ����У���������ֵ��4��
�ռ��ı���ABCD����������AC��BD���ഹֱ��AC��BD�ij��ֱ�Ϊ8��2����ƽ���ı�����������Ľ����ı���EFGH��ƽ�ƹ����У���������ֵ��4���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x+2y-5=0 | B�� | x-2y+3=0 | C�� | 2x+y-4=0 | D�� | 2x-y=0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | -1 | C�� | a+b+c | D�� | ab+bc+ca |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com