
【题目】已知两个不重合的平面α,β和两条不同直线m,n,则下列说法正确的是( )
A.若m⊥n,n⊥α,mβ,则α⊥β
B.若α∥β,n⊥α,m⊥β,则m∥n
C.若m⊥n,nα,mβ,则α⊥β
D.若α∥β,nα,m∥β,则m∥n
科目:高中数学 来源: 题型:
【题目】某工厂家具车间造A、B型两类桌子,每张桌子需木工和漆工两道工序完成.已知木工做一张A、B型桌子分别需要1小时和2小时,漆工油漆一张A、B型桌子分别需要3小时和1小时;又知木工、漆工每天工作分别不得超过8小时和9小时,而工厂造一张A、B型桌子分别获利润2千元和3千元,试问工厂每天应生产A、B型桌子各多少张,才能获得利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一位同学家里订了一份报纸,送报人每天都在在早上5:20~6:40之间将报纸送到达,该同学的爸爸需要早上6:00~7:00之间出发去上班,则这位同学的爸爸在离开家前能拿到报纸的概率是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(x∈R)的部分对应值如表:
x | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 |
y | ﹣6 | 0 | 4 | 6 | 6 | 4 | 0 | ﹣6 |
则一元二次不等式ax2+bx+c>0的解集是( )
A.{x|x<﹣2,或x>3}
B.{x|x≤﹣2,或x≥3}
C.{x|﹣2<x<3}
D.{x|﹣2≤x≤3}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为正方形,点E是棱PA的中点,PB=PD,平面BDE⊥平面ABCD. 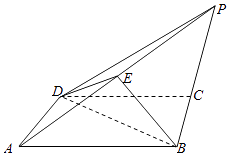
(Ⅰ)求证:PC∥平面BDE;
(Ⅱ)求证:PC⊥平面ABCD;
(Ⅲ)设PC=λAB,试判断平面PAD⊥平面PAB能否成立;若成立,写出λ的一个值(只需写出结论).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥 ![]() 中,底面ABCD是菱 形,PA=PB,且侧面PAB⊥平面ABCD,点E是AB的中点.
中,底面ABCD是菱 形,PA=PB,且侧面PAB⊥平面ABCD,点E是AB的中点.
(1)求证:PE⊥AD;
(2)若CA=CB,求证:平面PEC⊥平面PAB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的平行六面体ABCD﹣A1B1C1D中,AB=AD=AA1=1,∠BAD=90°,∠BAA1=∠DAA1=60°,则CA1的长= . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次马拉松比赛中,35名运动员的成绩(单位:分钟)的茎叶图如图所示.若将运动员成绩由好到差编号为1﹣35号,再用系统抽样方法从中抽取7人,则其中成绩在区间[139,151]上的运动员人数是 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com