
分析 (1)由题意可得sinC=$\frac{{\sqrt{3}}}{2}$,由锐角三角形可得C=60°;
(2)由余弦定理和基本不等式可得20=a2+b2-ab≥2ab-ab=ab,再由三角形的面积公式可得.
解答 解:(1)由2sin(A+B)-$\sqrt{3}$=0得sin(A+B)=$\frac{{\sqrt{3}}}{2}$,
即sin(π-C)=sinC=$\frac{{\sqrt{3}}}{2}$,
∵△ABC是锐角三角形,∴C=60°;
(2)由余弦定理得20=a2+b2-2ab•cos60°,即20=a2+b2-ab,
∵20=a2+b2-ab≥2ab-ab=ab(当且仅当a=b时,等号成立)
∴S△ABC=$\frac{1}{2}$ab•sin60°≤$\frac{1}{2}$×20×$\frac{{\sqrt{3}}}{2}$=$5\sqrt{3}$,
即S△ABC的最大值$5\sqrt{3}$.
点评 本题考查正余弦定理解三角形,涉及基本不等式和三角形的面积公式,属中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{18}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{5}{18}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -5 | B. | -2 | C. | 2 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年广东清远三中高二上学期第一次月考数学(理)试卷(解析版) 题型:解答题
已知动点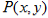 满足方程
满足方程 .
.
(Ⅰ)求动点P到直线 距离的最小值;
距离的最小值;
(Ⅱ)设定点 ,若点
,若点 之间的最短距离为
之间的最短距离为 ,求满足条件的实数
,求满足条件的实数 的取值.
的取值.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com