
分析 直线方程即 k(2x+y-1)+(-x+3y+11)=0,一定经过2x-y-1=0和-x-3y+11=0 的交点,联立方程组可求定点的坐标.
解答 解:直线(2k-1)x-(k+3)y-(k-11)=0
即 k(2x-y-1)+(-x-3y+11)=0,
根据k的任意性可得 $\left\{\begin{array}{l}{2x-y-1=0}\\{-x-3y+11=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$,
∴不论k取什么实数时,直线(2k-1)x+(k+3)y-(k-11)=0都经过一个定点(2,3).
故答案为:(2,3).
点评 本题考查经过两直线交点的直线系方程形式,直线 k(ax+by+c)+(mx+ny+p)=0 表示过ax+by+c=0和mx+ny+p=0的交点的一组相交直线,但不包括ax+by+c=0这一条.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
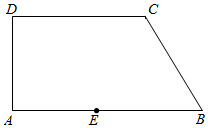 如图是一块直角梯形园地ABCD,AB∥CD,∠BAD=90°,经测最,AB=14m,CD=10m,∠ABC=60°,拟过线段AB上一点E设计一条直路EF(点F在四边形ABCD的边上,不计路的宽度),将该园地分为面积之比为3:1的左、石两部分分别种植不同花卉.设EB=x,EF=y(单位:m)
如图是一块直角梯形园地ABCD,AB∥CD,∠BAD=90°,经测最,AB=14m,CD=10m,∠ABC=60°,拟过线段AB上一点E设计一条直路EF(点F在四边形ABCD的边上,不计路的宽度),将该园地分为面积之比为3:1的左、石两部分分别种植不同花卉.设EB=x,EF=y(单位:m)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 日期 | 3月1日 | 3月2日 | 3月3日 | 3月4日 | 3月5日 | 3月6日 |
| 昼夜温差(℃) | 9 | 11 | 13 | 12 | 8 | 10 |
| 发芽数(粒) | 23 | 25 | 30 | 26 | 16 | 24 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com