
| 日期 | 3月1日 | 3月2日 | 3月3日 | 3月4日 | 3月5日 | 3月6日 |
| 昼夜温差(℃) | 9 | 11 | 13 | 12 | 8 | 10 |
| 发芽数(粒) | 23 | 25 | 30 | 26 | 16 | 24 |
分析 (1)根据平均数即可求出,
(2)一一列举出所有的基本事件,再找到满足条件的基本事件,根据概率公式计算即可.
解答 解:(1)这6天的平均发芽率为:$\frac{{\frac{23}{100}+\frac{25}{100}+\frac{30}{100}+\frac{26}{100}+\frac{16}{100}+\frac{24}{100}}}{6}×100%=24%$,
∴这6天的平均发芽率为 24%,
(2)(m,n)的取值情况有
$\begin{array}{l}(23,25),(23,30),(23,26),(23,16),(23,24),\\(25,30),(25,26),(25,16),(25,24),\\(30,26),(30,16),(30,24),\\(26,16),(26,24),\\(16,24),\end{array}$
事件数为15,
设$\left\{\begin{array}{l}25≤m≤30\\ 25≤n≤30\end{array}\right.$为事件A,则事件A包含的基本事件为(25,30),(25,26)(30,26),
∴所求概率$P=\frac{3}{15}=\frac{1}{5}$.
点评 本题考查了平均数,独立事件的概率计算,关键是列举,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -5 | B. | -2 | C. | 2 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3\sqrt{3}}{5}$ | B. | $\frac{4\sqrt{5}}{5}$ | C. | $\frac{5\sqrt{5}}{5}$ | D. | $\frac{6\sqrt{5}}{5}$ |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年广东清远三中高二上学期第一次月考数学(理)试卷(解析版) 题型:解答题
已知动点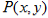 满足方程
满足方程 .
.
(Ⅰ)求动点P到直线 距离的最小值;
距离的最小值;
(Ⅱ)设定点 ,若点
,若点 之间的最短距离为
之间的最短距离为 ,求满足条件的实数
,求满足条件的实数 的取值.
的取值.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{1}{3}$,$\frac{3}{2}$] | B. | (-$\frac{1}{3}$,$\frac{3}{2}$] | C. | (-2,$\frac{3}{2}$] | D. | [$\frac{3}{2}$,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com