Question

12．已知两个半径为1的圆，圆心分别为O（0，0），C（m，0）（m≠0），圆O与圆C的公共弦经过点（$\frac{1}{2}$，0）．
（1）求m的值；
（2）若圆O的一条切线l交圆C于A、B两点，试判断|OA|•|OB|的值是否为定值？如果是，求出该定值；如果不是，请说明理由．

Answer 1

分析 （1）可得圆O：x²+y²=1，圆C：：（x-m）²+y²=1，两圆的公共弦方程为2mx-m²=0，由公共弦经过点（$\frac{1}{2}$，0），可得m=1；
（2）当切线l垂直x轴时，其方程为x=1，|OA|•|OB|=$\sqrt{2}$×$\sqrt{2}$=2，当切线l不垂直x轴时，设其方程为y=kx+b，A（x₁，y₁），B（x₂，y₂），y=kx+b与圆O相切，可得b²=1+k²
由$\left\{\begin{array}{l}{y=kx+b}\\{（x-1）^{2}+{y}^{2}=1}\end{array}\right.$得（1+k²）x²+（2kb-2）x+b²=0，${x}_{1}{x}_{2}=\frac{{b}^{2}}{1+{k}^{2}}$=1，即|OA|•|OB|=$\sqrt{{{x}_{1}}^{2}+{{y}_{1}}^{2}}$×$\sqrt{{{x}_{2}}^{2}+{{y}_{2}}^{2}}$=$\sqrt{2{x}_{1}}×\sqrt{2{x}_{2}}=2\sqrt{{x}_{1}{x}_{2}}$=2，综上，|OA|•|OB|的值是否为定值2．

解答 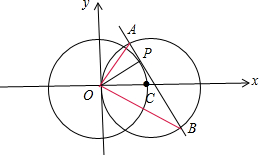解：（1）可得圆O：x²+y²=1，圆C：（x-m）²+y²=1，
两圆的公共弦方程为2mx-m²=0，
∵圆O与圆C的公共弦经过点（$\frac{1}{2}$，0）．且m≠0，
∴m=1．
（2）当切线l垂直x轴时，其方程为x=1，此时A（1，1），B（1，-1），
|OA|•|OB|=$\sqrt{2}$×$\sqrt{2}$=2，
当切线l不垂直x轴时，设其方程为y=kx+b，A（x₁，y₁），B（x₂，y₂），
∵y=kx+b与圆O相切，∴$\frac{|b|}{\sqrt{1+{k}^{2}}}=1$，即b²=1+k²，
由$\left\{\begin{array}{l}{y=kx+b}\\{（x-1）^{2}+{y}^{2}=1}\end{array}\right.$得（1+k²）x²+（2kb-2）x+b²=0，
∴${x}_{1}{x}_{2}=\frac{{b}^{2}}{1+{k}^{2}}$=1，
∵${（x}_{1}-1）^{2}+{{y}_{1}}^{2}=1$，：（x₂-m）²+y₂²=1，
∴${{x}_{1}}^{2}+{{y}_{1}}^{2}=2{x}_{1}$，${{x}_{2}}^{2}+{{y}_{2}}^{2}=2{x}_{2}$，
∴|OA|•|OB|=$\sqrt{{{x}_{1}}^{2}+{{y}_{1}}^{2}}$×$\sqrt{{{x}_{2}}^{2}+{{y}_{2}}^{2}}$=$\sqrt{2{x}_{1}}×\sqrt{2{x}_{2}}=2\sqrt{{x}_{1}{x}_{2}}$=2，
综上，|OA|•|OB|的值是否为定值2

点评 本题考查了圆的方程，圆与圆的位置关系，圆的切线，及直线与圆的位置关系，属于中档题．