Question

20．四边形ABCD为矩形，AB=2，BC=1，O为AB的中点，在矩形ABCD内随机取一点，取到的点到O的距离大于或等于1的概率为（　　）

• A． $\frac{π}{4}$
• B． 1-$\frac{π}{4}$
• C． $\frac{π}{8}$
• D． 1-$\frac{π}{8}$

Answer 1

分析 作出图形，在矩形ABCD内随机取一点，取到的点到O的距离大于或等于1包含的区域如图中阴影面积所示，由此利用几何概型能求出取到的点到O的距离大于或等于1的概率．

解答 解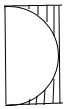：∵四边形ABCD为矩形，AB=2，BC=1，O为AB的中点，
∴作出图形如右图所示，
在矩形ABCD内随机取一点，
取到的点到O的距离大于或等于1包含的区域如图中阴影面积所示，
∴在矩形ABCD内随机取一点，
取到的点到O的距离大于或等于1的概率为：
p=$\frac{2×1-\frac{1}{2}×π×{1}^{2}}{2×1}$=1-$\frac{π}{4}$．
故选：B．

点评 本题考查概率的求法，考查几何概型等基础知识，考查数据处理能力、运算求解能力，考查化归与转化思想、函数与方程思想，是基础题．