Question

6．椭圆Г：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点分别为F₁，F₂，焦距为2c，若直线y=$\sqrt{3}$（x+c）与椭圆的一个交点满足∠MF₁F₂=2∠MF₂F₁，则该椭圆的离心率等于$\sqrt{3}-1$．

Answer 1

分析 在△MF₁F₂中，设∠MF₁F₂=60°，则∠MF₁F₁=30°，∠F₁MF₂=90°，由|F₁F₂|=2c，得|MF₁|=c，|MF₂|=$\sqrt{3}c$，从而2a=c+$\sqrt{3}c$，由此能求出该椭圆的离心率．

解答 解：椭圆Г：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点分别为F₁，F₂，焦距为2c，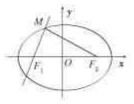
直线y=$\sqrt{3}$（x+c）与椭圆的一个交点满足∠MF₁F₂=2∠MF₂F₁，
如图，在△MF₁F₂中，设∠MF₁F₂=60°，则∠MF₁F₁=30°，∠F₁MF₂=90°，
∵|F₁F₂|=2c，∴|MF₁|=c，|MF₂|=$\sqrt{3}c$，
∴2a=|MF₁|+|MF₂|=c+$\sqrt{3}c$，
∴该椭圆的离心率e=$\frac{c}{a}=\frac{2}{\sqrt{3}+1}$=$\sqrt{3}-1$．
故答案为：$\sqrt{3}-1$．

点评 本题考查椭圆的离心率的求法，考查椭圆、直线方程等基础知识，考查推理论证能力、运算求解能力，考查化归与转化思想、函数与方程思想，考查创新意识、应用意识，是中档题．