
| A. | e | B. | 2 | C. | 3 | D. | e2 |
分析 设A(x1,m),B(x2,m),则x1+1=elogax2,表示出x1,求出|AB|,利用导数求出|AB|的最小值,即可得出结论.
解答 解:设A(x1,m),B(x2,m),则x1+1=elogax2,
∴x1=elogax2-1,
∴|AB|=x2-x1=x2-elogax2+1,
令y=x-elogax+1,则y′=1-$\frac{e}{xlna}$,
∴函数在(0,$\frac{e}{lna}$)上单调递减,在($\frac{e}{lna}$,+∞)上单调递增,
∴x=$\frac{e}{lna}$=e时,函数的最小值为1,
∴a=e
故选:A.
点评 本题考查导数知识的运用,考查学生分析解决问题的能力,正确求导确定函数的单调性是关键.


科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{e}$ | B. | 1 | C. | e | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 工作代码 | 工期/天 | 紧前工作 |
| A | 5 | 无 |
| B | 1 | A |
| C | 6 | A |
| D | 2 | A |
| E | 3 | B、C |
| F | 4 | B、C |
| 工作代码 | 工期/天 | 紧前工作 | 紧后工作 |
| A | 5 | 无 | |
| B | 1 | A | |
| C | 6 | A | |
| D | 2 | A | |
| E | 3 | B、C | |
| F | 4 | B、C |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
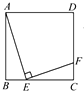 如图,已知正方形ABCD的边长为4,E是BC边上的一个动点,AE⊥EF,EF交DC于F,设BE=x,FC=y,则当点E从点B运动到点C时,y关于x的函数图象是( )
如图,已知正方形ABCD的边长为4,E是BC边上的一个动点,AE⊥EF,EF交DC于F,设BE=x,FC=y,则当点E从点B运动到点C时,y关于x的函数图象是( )| A. | 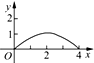 | B. | 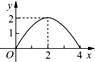 | C. | 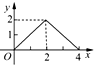 | D. | 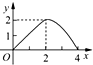 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-3<x≤4} | B. | {x|3<x<4} | C. | {x|3<x≤4} | D. | {x|-3<x<3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com