
(本小题满分13分)已知函数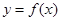
 .
.
(1)求函数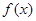 的最小正周期和最大值;
的最小正周期和最大值;
(2)在给出的直角坐标系中,画出函数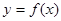 在区间
在区间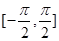 上的图象.
上的图象.
(3)设0<x<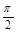 ,且方程
,且方程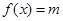 有两个不同的实数根,求实数m的取值范围.
有两个不同的实数根,求实数m的取值范围.
(1)函数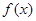 的最小正周期为
的最小正周期为 ,最大值为
,最大值为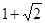 .
.
(2)函数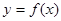 在区间
在区间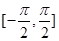 上的图象是
上的图象是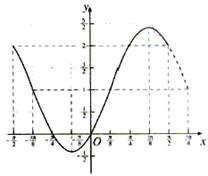
(3)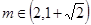 .
.
解析试题分析:(1)找出函数f(x)解析式中的ω的值,代入周期公式即可求出函数的最小正周期, 根据正弦函数的最大值为1,可知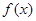 的最大值为
的最大值为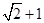 。
。
(2)利用五点法作出图像即可。其步骤为:列表,描点,连线。
(3)通过图像数形结合可知当直线y=m与y=f(x)在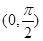 内有两个不同的实数根,
内有两个不同的实数根,
则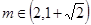 .
.
(1)所以函数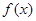 的最小正周期为
的最小正周期为 ,最大值为
,最大值为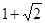 .
.
(2)由(1)知 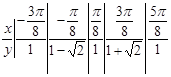
故函数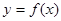 在区间
在区间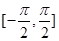 上的图象是
上的图象是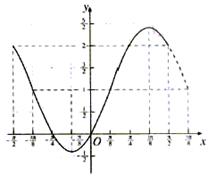
(3)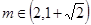 .
.
考点:函数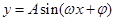 的图像及性质,五点法作图.
的图像及性质,五点法作图.
点评:借助正弦函数y=sinx的图像及性质掌握好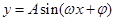 的图像及性质是解决此类问题的关键,其周期
的图像及性质是解决此类问题的关键,其周期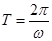 ,单调区间借助正弦函数的单调区间建立关于x的不等式求出解集即可。图像要利用五点法作图。
,单调区间借助正弦函数的单调区间建立关于x的不等式求出解集即可。图像要利用五点法作图。


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源: 题型:解答题
(本小题共12分)
已知函数f(t)= 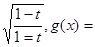
 ]
]
(Ⅰ)将函数g(x)化简成Asin(ωx+φ)+B(A>0,ω>0,φ∈[0,2π))的形式;
(Ⅱ)求函数g(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分13分)已知函数
(I)求函数f(x)的最小正周期和单调增区间;
(Ⅱ)函数f(x)的图象可以由函数y=sin2x(x∈R)的图象经过怎样的变换得到?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com