
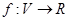 满足:对任意向量
满足:对任意向量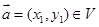
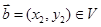 ,以及任意
,以及任意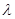 ∈R,均有
∈R,均有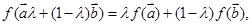 则称映射
则称映射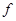 具有性质P.现给出如下映射:
具有性质P.现给出如下映射: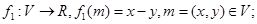
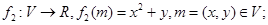
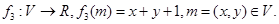


科目:高中数学 来源:不详 题型:单选题
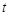 (月)与枝数
(月)与枝数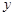 (枝)的散点图:那么“红豆生南国,春来发几枝.”的红豆生长时间与枝数的关系用下列哪个函数模型拟合最好? ( )
(枝)的散点图:那么“红豆生南国,春来发几枝.”的红豆生长时间与枝数的关系用下列哪个函数模型拟合最好? ( ) 
A.指数函数: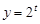 | B.对数函数: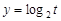 |
C.幂函数: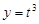 | D.二次函数: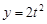 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
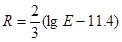 . 2011年3月11日,日本东海岸发生了9.0级特大地震,2008年中国汶川的地震级别为8.0级,那么2011年地震的能量是2008年地震能量的 倍;
. 2011年3月11日,日本东海岸发生了9.0级特大地震,2008年中国汶川的地震级别为8.0级,那么2011年地震的能量是2008年地震能量的 倍;查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
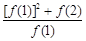 +
+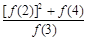 +
+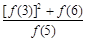 +
+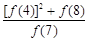 +
+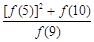 的值为_______________.
的值为_______________.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com