
| A. | y=$\frac{1}{1-x}$ | B. | y=cosx | C. | y=ln(x+1) | D. | y=2-x |
分析 根据函数单调性的定义,余弦函数单调性,以及指数函数的单调性便可判断每个选项函数在(-1,1)上的单调性,从而找出正确选项.
解答 解:A.x增大时,-x减小,1-x减小,∴$\frac{1}{1-x}$增大;
∴函数$y=\frac{1}{1-x}$在(-1,1)上为增函数,即该选项错误;
B.y=cosx在(-1,1)上没有单调性,∴该选项错误;
C.x增大时,x+1增大,ln(x+1)增大,∴y=ln(x+1)在(-1,1)上为增函数,即该选项错误;
D.$y={2}^{-x}=(\frac{1}{2})^{x}$;
∴根据指数函数单调性知,该函数在(-1,1)上为减函数,∴该选项正确.
故选D.
点评 考查根据单调性定义判断函数在一区间上的单调性的方法,以及余弦函数和指数函数的单调性,指数式的运算.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 乙盒中黑球不多于丙盒中黑球 | B. | 乙盒中红球与丙盒中黑球一样多 | ||
| C. | 乙盒中红球不多于丙盒中红球 | D. | 乙盒中黑球与丙盒中红球一样多 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
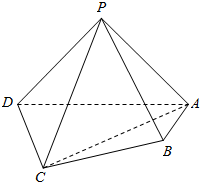 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC=CD=$\sqrt{5}$.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC=CD=$\sqrt{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com