
在 中,三个内角
中,三个内角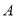 ,
,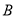 ,
,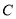 的对边分别为
的对边分别为 ,
, ,
,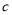 ,其中
,其中 ,且
,且
(1)求证: 是直角三角形;
是直角三角形;
(2)设圆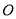 过
过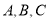 三点,点
三点,点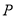 位于劣弧
位于劣弧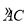 上,
上,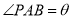 ,用
,用 的三角函数表示三角形
的三角函数表示三角形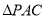 的面积,并求
的面积,并求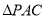 面积最大值.
面积最大值.
(1)祥见解析; (2)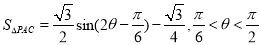 ;
;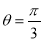 时,
时,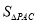 最大值等于
最大值等于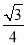 .
.
【解析】
试题分析:(1)利用正弦定理化简已知的等式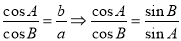 ,整理后再利用二倍角的正弦函数公式化简得到sin2A=sin2B,再利用正弦函数的图象与性质得到A与B相等或A与B互余,由b与a的比值不相等,得到A不等于B,故A与B互余,可得出C为直角,则此三角形为直角三角形,得证;
,整理后再利用二倍角的正弦函数公式化简得到sin2A=sin2B,再利用正弦函数的图象与性质得到A与B相等或A与B互余,由b与a的比值不相等,得到A不等于B,故A与B互余,可得出C为直角,则此三角形为直角三角形,得证;
(2)由三角形ABC为直角三角形,根据a与b的比值,以及c的值,利用勾股定理求出a与b的值,再由一条直角边等于斜边的一半,可得出此直角边所对的角为30°,即∠BAC为30°,又∠PAB=θ,用∠PAB-∠BAC表示出∠PAC,同时在直角三角形PAB中,由AB的长及∠PAB=θ,利用锐角三角函数定义表示出PA,由AC,PA及sin∠PAC,利用三角形的面积公式表示出三角形APC的面积,利用特殊角的三角函数值及两角和与差的正弦函数公式化简,整理后利用二倍角的正弦、余弦函数公式化简,最后利用两角和与差的正弦函数公式及特殊角的三角函数值化为一个角的正弦函数,根据θ的范围,求出这个角的范围,根据正弦函数的图象与性质可得出正弦函数的值域,进而确定出面积的最大值.
试题解析:(1)证明:由正弦定理得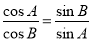 ,整理为
,整理为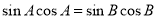 ,即sin2A=sin2B ∴2A=2B或2A+2B=π,即A=B或A+B=
,即sin2A=sin2B ∴2A=2B或2A+2B=π,即A=B或A+B=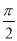 ∵
∵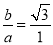 ,∴A=B舍去.由A+B=
,∴A=B舍去.由A+B=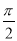 可知c=
可知c=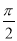 ,∴ΔABC是直角三角形
,∴ΔABC是直角三角形
(2)由(1)及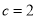 ,得
,得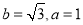 , 在RtΔ
, 在RtΔ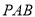 中,
中,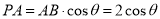 所以,
所以,
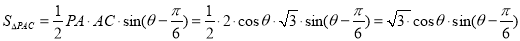
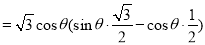
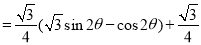
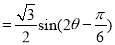
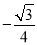 ,
,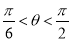 因为
因为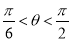 ,所以,
,所以,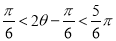
当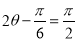 ,即
,即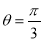 时,
时,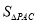 最大值等于
最大值等于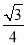
考点:1.正弦定理;2.两角和与差的正弦函数;3.正弦函数的定义域和值域.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源:2015届河南省高二实验班上学期期中考试数学试卷(解析版) 题型:选择题
已知函数f(x)= ,若方程f(x)+2a-1=0恰有4个实数根,则实数a的取值范围是 ( )
,若方程f(x)+2a-1=0恰有4个实数根,则实数a的取值范围是 ( )
(A)(- ,0 ] (B)[-
,0 ] (B)[- ,0 ]
,0 ]
(C)[1, ) (D)(1,
) (D)(1, ]
]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com