练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数f（x）对任意x∈R都有f（x+6）+f（x）=2f（3），y=f（x﹣1）的图象关于点（1，0）对称，则f（2013）=（　　）

      A.10                 B.-5             C.5            D.0


    D

    【解析】由f（x+6）+f（x）=2f（3），知f（x+12）+f（x+6）=2f（3），两式相减，得f（x+12）=f（x）

    由y=f（x﹣1）的图象关于点（1，0）对称，知f（x﹣1）+f（1﹣x）=0，故f（x）是奇函数．

    由f（x+6）+f（x）=2f（3），令x=﹣3，得f（3）=f（﹣3），于是f（3）=f（﹣3）=0，

    于是f（2013）=f（2013﹣12×167）=f（9）=f（﹣3）=0

    故选D．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


     运行右图所示框图的相应程序,若输入的值分别为和,则输出M的值是（    ）

    A.0      B.1     C. 2      D. －1

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设某中学高三的女生体重y（单位：kg）与身高x（单位：cm）具有线性相关关系，根据一组样本数据（xi，yi）（i=1，2，…，n），用最小二乘法建立的回归方程为y=0.85x﹣85.71，则下列结论中不正确的是（　　）

      A. y与x具有正的线性相关关系

      B. 回归直线过样本点的中心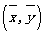

      C. 若该中学高三某女生身高增加1cm，则其体重约增加0.85kg

      D. 若该中学高三某女生身高为170cm，则可断定其体重必为58.79kg

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某校举行中学生“日常生活小常识”知识比赛,比赛分为初赛和复赛两部分，初赛采用选手从备选题中选一题答一题的方式进行；每位选手最多有5次答题机会，选手累计答对3题或答错3题即终止比赛，答对3题者直接进入复赛，答错3题者则被淘汰.已知选手甲答对每个题的概率均为，且相互间没有影响.

    (1) 求选手甲进入复赛的概率；

    (2) 设选手甲在初赛中答题的个数为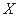，试求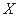的分布列和数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图是某一几何体的三视图，则这个几何体的体积为（　　）

    　

    A．

    4

    B．

    8

    C．

    16

    D．

    20

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知集合A={f（x）|f2（x）﹣f2（y）=f（x+y）•f（x﹣y），x、y∈R}，有下列命题：

    ①若f（x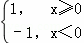）=，则f（x）∈A；

    ②若f（x）=kx，则f（x）∈A；

    ③若f（x）∈A，则y=f（x）可为奇函数；

    ④若f（x）∈A，则对任意不等实数x1，x2，总有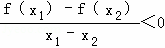成立．

    其中所有正确命题的序号是　______　．（填上所有正确命题的序号）

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    不等式的解是                 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


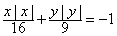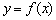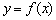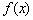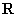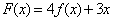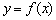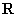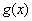    方程的曲线即为函数的图像，对于函数，有如下结论：①在上单调递减；②函数不存在零点；③函数的值域是；④若函数和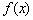的图像关于原点对称，则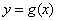由方程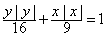确定．其中所有正确的命题序号是           [答]（    ）

    (A) ①③．         (B) ①④．        (C) ①③④．       (D) ①②③．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知，对，使得，则的最小值为（   ）

    A.           B.          C.        D.

    查看答案和解析>>

    同步练习册答案