
【题目】(Ⅰ)求平行于直线x﹣2y+1=0,且与它的距离为2 ![]() 的直线方程; (Ⅱ)求经过两直线l1:x﹣2y+4=0和l2:x+y﹣2=0的交点P,且与直线l3:2x+3y+1=0垂直的直线l的方程.
的直线方程; (Ⅱ)求经过两直线l1:x﹣2y+4=0和l2:x+y﹣2=0的交点P,且与直线l3:2x+3y+1=0垂直的直线l的方程.
【答案】解:(Ⅰ)设与直线x﹣2y+1=0平行的直线方程为x﹣2y+c=0, 在直线x﹣2y+1=0上任取一点P(1,1),
依题意P到直线x﹣2y+c=0的距离为 ![]() ,解得:c=11或c=﹣9
,解得:c=11或c=﹣9
所求直线方程为:x﹣2y+11=0或x﹣2y﹣9=0
(Ⅱ)法一:由方程组 ![]() ,得
,得 ![]() ,
,
即P(0,2).l3:2x+3y+1=0的斜率为 ![]()
∵l⊥l3 , ∴ ![]() ,(l3斜率(1分),k3k=﹣(11分),结论1分)
,(l3斜率(1分),k3k=﹣(11分),结论1分)
∴直线l的方程为 ![]() ,
,
即l:3x﹣2y+4=0.
法二:∵直线l过直线l1和l2的交点,
∴可设直线l的方程为x﹣2y+4+λ(x+y﹣2)=0,
即(1+λ)x+(λ﹣2)y+4﹣2λ=0.l3:2x+3y+1=0的斜率为 ![]()
∵l⊥l3 , ∴ ![]() ,
,
∴3(λ﹣2)+2(λ+1)=0,
∴λ= ![]() ,
,
∴直线l的方程为3x﹣2y+4=0,(对照解法一相应给分)
【解析】(Ⅰ)根据直线平行和平行线的距离求出满足条件的直线方程即可;(Ⅱ)法一:根据方程组求出P的坐标,结合直线垂直的关系求出满足条件的直线方程即可; 法二:根据直线平行,设直线l的方程为x﹣2y+4+λ(x+y﹣2)=0,根据直线的垂直关系求出直线的斜率,求出参数的值,从而求出直线方程即可.


科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =3
=3 ![]() 1﹣2
1﹣2 ![]() 2 ,
2 , ![]() =4
=4 ![]() 1+
1+ ![]() 2 , 其中
2 , 其中 ![]() 1=(1,0),
1=(1,0), ![]() 2=(0,1),求:
2=(0,1),求:
(1)![]()
![]() 和|
和| ![]() +
+ ![]() |的值;
|的值;
(2)![]() 与
与 ![]() 夹角θ的余弦值.
夹角θ的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知,圆C:x2+y2﹣8y+12=0,直线l:ax+y+2a=0.
(1)当a为何值时,直线l与圆C相切;
(2)当直线l与圆C相交于A,B两点,且AB=2 ![]() 时,求直线l的方程.
时,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2﹣8y+12=0,直线l经过点D(﹣2,0),且斜率为k.
(1)求以线段CD为直径的圆E的方程;
(2)若直线l与圆C相离,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在斜三棱柱ABC﹣A1B1C1中,∠BAC=90°,BC1⊥AC,则C1在面ABC上的射影H必在( ) 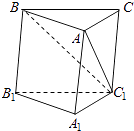
A.直线AB上
B.直线BC上
C.直线CA上
D.△ABC内部
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省每年损失耕地20万亩,每亩耕地价值24000元,为了减少耕地损失,决定按耕地价格的t%征收耕地占用税,这样每年的耕地损失可减少 ![]() t万亩,为了既可减少耕地的损失又保证此项税收一年不少于9000万元,则t的取值范围是( )
t万亩,为了既可减少耕地的损失又保证此项税收一年不少于9000万元,则t的取值范围是( )
A.[1,3]
B.[3,5]
C.[5,7]
D.[7,9]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数y=f(x)的图象上每一点的纵坐标保持不变,横坐标伸长到原来的2倍,再将整个图象沿x轴向右平移 ![]() 个单位,沿y轴向下平移1个单位,得到函数y=
个单位,沿y轴向下平移1个单位,得到函数y= ![]() sinx的图象,则y=f(x)的解析式为( )
sinx的图象,则y=f(x)的解析式为( )
A.y= ![]() sin(2x+
sin(2x+ ![]() )+1
)+1
B.y= ![]() sin(2x﹣
sin(2x﹣ ![]() )+1
)+1
C.y= ![]() sin(
sin( ![]() x+
x+ ![]() )+1
)+1
D.y= ![]() sin(
sin( ![]() x﹣
x﹣ ![]() )+1
)+1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com