
分析 (1)利用二倍角公式以及两角和与差的三角函数化简函数的解析式,然后求解函数的周期以及函数的最值.
(2)利用正弦函数的单调区间,转化求解即可.
解答 解:(1)$y={cos^2}x+\sqrt{3}sinxcosx+1=\frac{cos2x+1}{2}+\frac{{\sqrt{3}sin2x}}{2}+1=\frac{1}{2}cos2x+\frac{{\sqrt{3}}}{2}sin2x+\frac{1}{2}+1$=$sin\frac{π}{6}cos2x+cos\frac{π}{6}sin2x+\frac{3}{2}=sin({2x+\frac{π}{6}})+\frac{3}{2}$.
函数的最小正周期:π;最大值为:$\frac{5}{2}$,最小值为:$\frac{1}{2}$.
(2)因为函数y=sinx的单调递增区间为$[{-\frac{π}{2}+2kπ,\frac{π}{2}+2kπ}]({k∈Z})$,
由(1)知$y=sin({2x+\frac{π}{6}})+\frac{3}{2}$,故$-\frac{π}{2}+2kπ≤2x+\frac{π}{6}≤\frac{π}{2}+2kπ({k∈Z})$,
∴$-\frac{π}{3}+kπ≤x≤\frac{π}{6}+kπ({k∈Z})$,
故函数$y=sin({2x+\frac{π}{6}})+\frac{3}{2},0<x<π$的单调递增区间为$({0,\frac{π}{6}}]$和$[{\frac{2π}{3},π})$;
单调递减区间为$[{\frac{π}{6},\frac{2π}{3}}]$.
点评 本题考查两角和与差的三角函数,三角函数的最值的求法正确的求法,考查计算能力.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | y=[$\frac{x}{10}$] | B. | y=[$\frac{x+2}{10}$] | C. | y=[$\frac{x+3}{10}$] | D. | y=[$\frac{x+4}{10}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0<x≤2} | B. | {0,1,2} | C. | {1,2} | D. | {1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{2}$ | B. | 2 | C. | $\frac{3}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | -3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
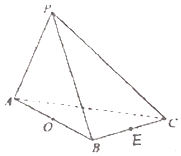 在三棱锥P-ABC中,△PAC和△PBC是边长为$\sqrt{2}$的等边三角形,AB=2,O是AB中点,E是BC中点.
在三棱锥P-ABC中,△PAC和△PBC是边长为$\sqrt{2}$的等边三角形,AB=2,O是AB中点,E是BC中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com