
分析 (1)根据曲线y=f(x)与曲线y=g(x)在它们的交点(1,c)处具有公共切线,可知切点处的函数值相等,切点处的斜率相等,故可求a、b的值;
(2)根据a2=4b,构建函数$h(x)=f(x)+g(x)={x^3}+a{x^2}+\frac{1}{4}{a^2}x+1$,求导函数,利用导数的正负,可确定函数的单调区间,进而分类讨论,确定函数在区间(-∞,-1)上的最大值.
解答 解:(1)由(1,c)公共切点可得:f(x)=ax2+1(a>0),
则f'(x)=2ax,k1=2a,g(x)=x3+bx,
则g'(x)=3x2+b,k2=3+b,∴2a=3+b①
又f(1)=a+1,g(1)=1+b,∴a+1=1+b,即a=b,代入①式可得:$\left\{\begin{array}{l}a=3\\ b=3\end{array}\right.$.
(2)∵a2=4b,∴设$h(x)=f(x)+g(x)={x^3}+a{x^2}+\frac{1}{4}{a^2}x+1$
则$h'(x)=3{x^2}+2ax+\frac{1}{4}{a^2}$,
令h'(x)=0,解得:${x_1}=-\frac{a}{2}$,${x_2}=-\frac{a}{6}$;
∵a>0,∴$-\frac{a}{2}<-\frac{a}{6}$,
∴原函数在$({-∞\;,\;\;-\frac{a}{2}})$单调递增,在$({-\frac{a}{2}\;,\;\;-\frac{a}{6}})$单调递减,在$({-\frac{a}{6}\;,\;\;+∞})$上单调递增
①若$-1≤-\frac{a}{2}$,即a≤2时,最大值为$h(1)=a-\frac{a^2}{4}$;
②若$-\frac{a}{2}<-1<-\frac{a}{6}$,即2<a<6时,最大值为$h({-\frac{a}{2}})=1$
③若$-1≥-\frac{a}{6}$时,即a≥6时,最大值为$h({-\frac{a}{2}})=1$.
综上所述:当a∈(0,2]时,最大值为$h(1)=a-\frac{a^2}{4}$;当a∈(2,+∞)时,最大值为$h({-\frac{a}{2}})=1$.
点评 本题考查导数知识的运用,考查导数的几何意义,考查函数的单调性与最值,解题的关键是正确求出导函数.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
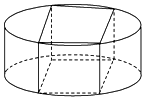 将一个底面圆的直径为2、高为1的圆柱截成一个长方体,如图所示,设这个长方体底面的一条边长为x、对角线长为2,底面的面积为A.
将一个底面圆的直径为2、高为1的圆柱截成一个长方体,如图所示,设这个长方体底面的一条边长为x、对角线长为2,底面的面积为A.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com