练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    9．设Sn=1+3+5+…+（2n-1）（n∈N*），则f（n）=$\frac{（n+8）（n+2）}{\sqrt{{S}_{n}}}$的最小值为（　　）
    A．9B．12C．18D．24

    分析 由等差数列的前n项和求得Sn，代入f（n）=$\frac{（n+8）（n+2）}{\sqrt{{S}_{n}}}$后利用基本不等式求最值．

    解答 解：∵Sn=1+3+5+…+（2n-1）=$\frac{（1+2n-1）n}{2}={n}^{2}$，
    ∴f（n）=$\frac{（n+8）（n+2）}{\sqrt{{S}_{n}}}$=$\frac{{n}^{2}+10n+16}{n}=n+\frac{16}{n}+10$$≥2\sqrt{n•\frac{16}{n}}+10=18$．
    上式当且仅当n=4时取等号．
    故选：C．

    点评 本题考查等差数列的前n项和，考查了利用基本不等式求最值，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    12．设A，B是双曲线x2-y2=1上关于原点O对称的两点，将坐标平面沿双曲线的一条渐近线l折成直二面角，则折叠后线段AB长度的最小值为（　　）
    A．$\sqrt{2\sqrt{2}}$B．$\sqrt{3\sqrt{2}}$C．$\sqrt{2}$D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．假如今年省运会给岭师附中高中三个年级7个自主推荐的志愿者名额，则每个年级至少分到一个名额的方法数为（　　）
    A．10B．15C．21D．30

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．直线y=m分别与曲线y=2x+3，y=x+lnx交于A、B，则|AB|的最小值为（　　）
    A．$\frac{3}{2}$B．$\frac{3\sqrt{2}}{4}$C．2D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．已知函数y=f（-|x|）的图象如图所示，则函数y=f（x）的图象不可能是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．求函数y=tan（$\frac{π}{3}$x+$\frac{π}{4}$）的定义域、周期、单调区间和对称中心．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．求log89log32-lg4-lg25的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．设函数f（x）=$\left\{\begin{array}{l}{{2}^{x+4}，x≤4}\\{-lo{g}_{2}（x+1），x＞4}\end{array}\right.$，若f（a）=$\frac{1}{8}$．求f[f（a+6）]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

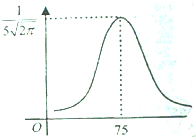    19．某市高二理科学生数学考试的成绩x服从正态分布，其密度函数为f（x）=$\frac{1}{\sqrt{2π}σ}$e${\;}^{\frac{（x-μ）^{2}}{2{σ}^{2}}}$，密度曲线如图，已知该市理科学生总数是10000人，则成绩位于（65，85]的人数约是9544．

    查看答案和解析>>

    同步练习册答案