
(1)m为何值时,f(x)=x2+2mx+3m+4.
①有且仅有一个零点;②有两个零点且均比-1大;
(2)若函数f(x)=|4x-x2|+a有4个零点,求实数a的取值范围.
(1) ① m=4或m=-1;②(-5,-1);(2) (-4,0).
解析试题分析:(1) ①由函数的零点与方程根之间的关系可知函数f(x)=x2+2mx+3m+4有且仅有一个零点,等价于方程f(x)=0有两个相等实根,而此方程是关于x的一元二次方程,所以其判别式Δ=0,从而可求得m的值;②函数f(x)=x2+2mx+3m+4有两个零点且均比-1大,结合二次函数图象可知首先其判别式应大于零,同时其对称轴应在-1的右侧,并且函数在-1的函数值大于零;从而获得一个关于m的不等式组,解此不等式组即可求得m的取值范围;(2) 函数f(x)=|4x-x2|+a有4个零点等价于|4x-x2|=-a,也即函数g(x)=|4x-x2|的图象与直线y=-a有四个不同的交点,作出图象即可求出a的取值范围.
试题解析:(1)①f(x)=x2+2mx+3m+4有且仅有一个零点,即方程f(x)=0有两个相等实根,亦即Δ=0,即4m2-4(3m+4)=0,即m2-3m-4=0,∴m=4或m=-1.
②由题意,知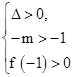
即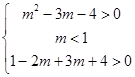
∴-5<m<-1.
∴m的取值范围为(-5,-1).
(2)令f(x)=0,得|4x-x2|+a=0,
即|4x-x2|=-a.
令g(x)=|4x-x2|,h(x)=-a.
作出g(x)、h(x)的图象.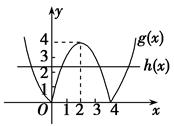
由图象可知,当0<-a<4,即-4<a<0时,g(x)与h(x)的图象有4个交点,即f(x)有4个零点.故a的取值范围为(-4,0).
考点:1.函数零点的概念;2.函数的零点与方程的根及函数图象交点之间的关系.


科目:高中数学 来源: 题型:填空题
设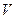 是已知平面
是已知平面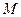 上所有向量的集合,对于映射
上所有向量的集合,对于映射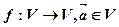 ,记
,记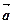 的象为
的象为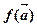 。若映射
。若映射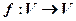 满足:对所有
满足:对所有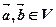 及任意实数
及任意实数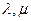 都有
都有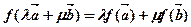 ,则
,则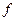 称为平面
称为平面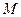 上的线性变换。现有下列命题:
上的线性变换。现有下列命题:
①设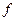 是平面
是平面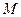 上的线性变换,则
上的线性变换,则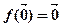
②对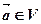 设
设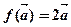 ,则
,则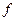 是平面
是平面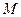 上的线性变换;
上的线性变换;
③若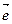 是平面
是平面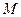 上的单位向量,对
上的单位向量,对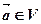 设
设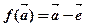 ,则
,则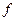 是平面
是平面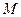 上的线性变换;
上的线性变换;
④设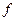 是平面
是平面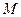 上的线性变换,
上的线性变换,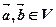 ,若
,若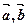 共线,则
共线,则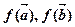 也共线。
也共线。
其中真命题是 (写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数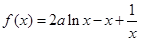 (
( 且
且 ),
),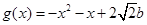
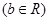 .
.
(1)若 在定义域上有极值,求实数
在定义域上有极值,求实数 的取值范围;
的取值范围;
(2)当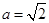 时,若对
时,若对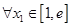 ,总
,总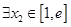 ,使得
,使得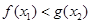 ,求实数
,求实数 的取值范围;(其中
的取值范围;(其中 为自然对数的底数)
为自然对数的底数)
(3)对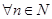 ,且
,且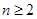 ,证明:
,证明: 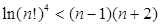 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com