已知函数
是定义在
上的增函数，对于任意的
，都有
，且满足
．
（1）求
的值;
（2）求满足
的
的取值范围．
阅读快车系列答案科目：高中数学 来源： 题型：填空题
给出下列命题：
①函数
为非零常数）的图象可由函数y=3x的图象经过平移得到；
②函数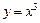
在R上既是奇函数又是增函数.
③不等式
④函数
至多有一个交点.
⑤若定义在R上的函数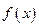
满足
,则函数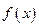是周期函数.
⑥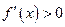
在定义域内恒成立函数
在定义域内单调递增的充分不必要条件.
其中正确命题的序号是 .（把你认为正确命题的序号都填上）
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
(1)m为何值时，f(x)＝x2＋2mx＋3m＋4.
①有且仅有一个零点；②有两个零点且均比－1大；
(2)若函数f(x)＝|4x－x2|＋a有4个零点，求实数a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知函数f(x)对任意实数x，y恒有f(x＋y)＝f(x)＋f(y)，且当x>0时，f(x)<0，又f(1)＝－2.
(1)判断f(x)的奇偶性；
(2)求证：f(x)是R上的减函数；
(3)求f(x)在区间[－3,3]上的值域；
(4)若?x∈R，不等式f(ax2)－2f(x)<f(x)＋4恒成立，求a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：填空题
某地街道呈现东—西、南—北向的网格状，相邻街距都为1.两街道相交的点称为格点.若以互相垂直的两条街道为轴建立直角坐标系，现有下述格点
，
，
，
，
，
为报刊零售点.请确定一个格点（除零售点外）__________为发行站，使6个零售点沿街道到发行站之间路程的和最短.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
；（2）
．
进行赋值求解即可；（2）将
，利用函数的单调性解不等式．
的形式，则利用函数的单调性进行化简求解．
，得
， 则
，
，得
， 则
，故
，解得
（
，
），
．
的单调区间，并确定其零点个数；
在其定义域内单调递增，求
的取值范围；
（
）．
的定义域为
，
.
，求实数
的取值范围.
，则
的值等于 ．