练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    13．已知3A${\;}_{8}^{n}$=4A${\;}_{9}^{n-1}$，求n的值．

    分析 由已知条件利用排列数公式，得3×8×7×…×（9-n）=4×9×8×7×…×（11-n），由此能求出m．

    解答 解：∵3A8n=4A9n-1，
    ∴3×8×7×…×（9-n）=4×9×8×7×…×（11-n），
    ∴3（10-n）（11-n）=4×9，
    整理，得n2-21n+98=0，
    解得n=7或n=14（舍），
    ∴n=7．

    点评 本题考查实数值的求法，是基础题，解题时要认真审题，注意排列数公式的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    3．在O点测量到远处有一物体在做匀速直线运动，开始时该物体位于P点，一分钟后，其位置在Q点，且∠POQ=90°，再过两分钟后，该物体位于R点，且∠QOR=30°，则tan∠OPQ的值为$\frac{2\sqrt{3}}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．已知△ABC中，内角A，B，C所对的边长分别为a，b，c．若a=2bcosA，B=$\frac{π}{3}$，c=1，则△ABC的面积等于（　　）
    A．$\frac{{\sqrt{3}}}{8}$B．$\frac{{\sqrt{3}}}{6}$C．$\frac{{\sqrt{3}}}{4}$D．$\frac{{\sqrt{3}}}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．在平面直角坐标系中，把横、纵坐标均为有理数的点称为有理点．若a为无理数，则在过点P（a，-$\frac{1}{2}$）的所有直线中（　　）
    A．有无穷多条直线，每条直线上至少存在两个有理点
    B．恰有n（n≥2）条直线，每条直线上至少存在两个有理点
    C．有且仅有一条直线至少过两个有理点
    D．每条直线至多过一个有理点

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知m≥0，函数f（x）=2|x-1|-|2x+m|的最大值为3．
    （Ⅰ）求实数m的值；
    （Ⅱ）若实数a，b，c满足a-2b+c=m，求a2+b2+c2的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．设函数f（x）=a2x2（a＞0），g（x）=blnx．
    （1）若函数y=f（x）图象上的点到直线x-y-3=0距离的最小值为2$\sqrt{2}$，求a的值；
    （2）关于x的不等式（x-1）2＞f（x）的解集中的整数恰有3个，求实数a的取值范围；
    （3）对于函数f（x）与g（x）定义域上的任意实数x，若存在常数k，m，使得f（x）≥kx+m和g（x）≤kx+m都成立，则称直线y=kx+m为函数f（x）与g（x）的“分界线”．设a=$\frac{\sqrt{2}}{2}$，b=e，试探究f（x）与g（x）是否存在“分界线”？若存在，求出“分界线”的方程；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

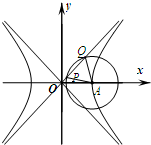    5．如图，已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右顶点为A，O为坐标原点，以A为圆心的圆与双曲线C的某渐近线交于两点P，Q．若∠PAQ=60°且$\overrightarrow{OQ}$=4$\overrightarrow{OP}$，则双曲线C的离心率为（　　）
    A．$\sqrt{3}$B．$\frac{2\sqrt{13}}{5}$C．$\frac{\sqrt{7}}{2}$D．$\frac{2\sqrt{3}}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．下列四个命题中正确命题的是（　　）
    A．学校抽取每个班级座号为21-30号的同学检查作业完成情况，这是分层抽样
    B．可以通过频率分布直方图中最高小矩形的高来估计这组数据的众数
    C．设随机变量ξ服从正态分布N（0，1），若P（ξ＞1）=p，则P（-1＜ξ＜0）=1-p
    D．在散点图中，回归直线至少经过一个点

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．若集合A={x|2${\;}^{{x}^{2}-4x-5}$＞1}，集合B={x|y=lg$\frac{2-x}{2+x}$}，则A∩B=（　　）
    A．{x|-5＜x＜1}B．{x|-2＜x＜1}C．{x|-2＜x＜-1}D．{x|-5＜x＜-1}

    查看答案和解析>>

    同步练习册答案