
分析 利用正弦定理分别在△RQO和△RPO中分别表示出OQ和OP,进而根据tan∠OPQ=$\frac{OQ}{OP}$求得答案.
解答 
解:依题意可知RQ=2QP,
在△RQO中,$\frac{OQ}{sinR}$=$\frac{RQ}{sin30°}$,
OQ=$\frac{RQ}{sin30°}$•sinR,
同理在△RPO中,OP=$\frac{RP}{sin120°}$•sinR,
tan∠OPQ=$\frac{OQ}{OP}$=$\frac{\frac{RQ}{sin30°}}{\frac{RP}{sin120°}}$=$\frac{RQ}{sin30°}$•$\frac{sin120°}{RP}$=$\frac{2}{3}$×$\frac{\frac{\sqrt{3}}{2}}{\frac{1}{2}}$=$\frac{2\sqrt{3}}{3}$.
点评 本题主要考查了正弦定理的运用.解决问题的关键是运用sinR作为中间量来解决.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a17=0 | B. | a6+a12=0 | C. | S17>0 | D. | a9<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
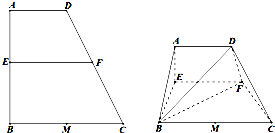 已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=90°,AB=BC=2AD=4,M是BC边的中点,E,F分别是AB,CD上的点,且EF∥BC,设AE=x.如图,沿EF将四边形AEFD折起,使平面AEFD⊥平面EBCF.
已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=90°,AB=BC=2AD=4,M是BC边的中点,E,F分别是AB,CD上的点,且EF∥BC,设AE=x.如图,沿EF将四边形AEFD折起,使平面AEFD⊥平面EBCF.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,2] | B. | (-1,2) | C. | [-1,2] | D. | (-2,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | |a+b|>|a-b| | B. | |a|+|b|>|a-b| | C. | |a-c|≤|a-b|+|b-c| | D. | |a-b|<|a|-|b| |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com