
分析 求解导数g′(x)=ex+1$-\frac{1}{x}$,根据性质得出g(x)在[$\frac{1}{2}$,+∞)上是单调递增;构造函数G(x)=$\frac{g(x)}{x}$,G′(x)=$\frac{x{e}^{x}-{e}^{x}-2+lnx}{{x}^{2}}$,x>0,
设m(x)=xex-ex-2+lnx,再次求解导数得出m′(x)=xex$+\frac{1}{x}$>0,m(x)在(0,+∞)上单调递增,利用特殊值判断m($\frac{1}{2}$)=$-\frac{1}{2}$e${\;}^{\frac{1}{2}}$-2-ln2<0,m(1)=e-e-2+0=-2<0,m($\frac{3}{2}$)=$\frac{1}{2}$e${\;}^{\frac{3}{2}}$-2+ln($\frac{3}{2}$)>0(根据图象判断),确定在[$\frac{3}{2}$,+∞)上,有G′(x)=$\frac{x{e}^{x}-{e}^{x}-2+lnx}{{x}^{2}}$>0成立,函数G(x)=$\frac{g(x)}{x}$在[$\frac{3}{2}$,+∞)上是单调递增函数.再考虑函数g(x)是区间$[\frac{m}{2},+∞)$上的“完美函数”,定义,判断出整数m的最小值.
解答 解:∵g(x)=ex+x-lnx+1,x>0,
∴g′(x)=ex+1$-\frac{1}{x}$在(0,+∞)单调递增,g′($\frac{1}{2}$)=$\sqrt{e}$-1>0,
∴可以得出:g(x)在[$\frac{1}{2}$,+∞)上是单调递增.
∵G(x)=$\frac{g(x)}{x}$,G′(x)=$\frac{x{e}^{x}-{e}^{x}-2+lnx}{{x}^{2}}$,x>0,
设m(x)=xex-ex-2+lnx,
m′(x)=xex$+\frac{1}{x}$>0,m(x)在(0,+∞)上单调递增,
m($\frac{1}{2}$)=$-\frac{1}{2}$e${\;}^{\frac{1}{2}}$-2-ln2<0,
m(1)=e-e-2+0=-2<0,
m($\frac{3}{2}$)=$\frac{1}{2}$e${\;}^{\frac{3}{2}}$-2+ln($\frac{3}{2}$)>0(根据图象判断)
∴在[$\frac{3}{2}$,+∞)上,有G′(x)=$\frac{x{e}^{x}-{e}^{x}-2+lnx}{{x}^{2}}$>0成立,
∴函数G(x)=$\frac{g(x)}{x}$在[$\frac{3}{2}$,+∞)上是单调递增函数,
综合判断:g(x)=ex+x-lnx+1,与G(x)=$\frac{g(x)}{x}$在[$\frac{3}{2}$,+∞)上都是单调递增函数,
g(x)=ex+x-lnx+1,与G(x)=$\frac{g(x)}{x}$在[1,+∞)上不是都为单调递增函数,
∵函数g(x)是区间$[\frac{m}{2},+∞)$上的“完美函数”,整数m.
∴m≥3,
即最小值为3.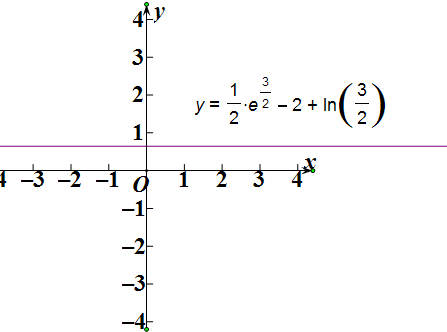
故答案为:3
点评 本题以新定义的形式考查函数的单调性,考查运用所学知识分析解决新问题的能力,多次构造函数,求解导数,判断的递增,思路要清晰,属于难题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
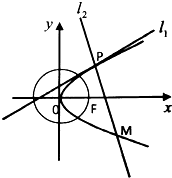 如图,已知圆O:x2+y2=a2(a>0)过抛物线C:y2=2px(p>0)的焦点F,过点F且与圆O相切的直线被抛物线C截得的弦长为4
如图,已知圆O:x2+y2=a2(a>0)过抛物线C:y2=2px(p>0)的焦点F,过点F且与圆O相切的直线被抛物线C截得的弦长为4查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 2 | C. | 4 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com