练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    12．如图是一个几何体的三视图，则该几何体的体积为36$\sqrt{3}$（π+2）．

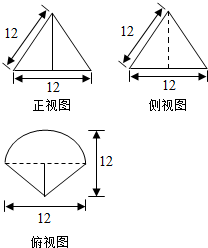
    分析 由已知中的三视图，可知该几何体是一个以俯视图为底面的锥体，分别计算底面面积和高，代入锥体体积公式，可得答案．

    解答 解：由已知中的三视图，可知该几何体是一个以俯视图为底面的锥体，
    其底面面积S=$\frac{1}{2}$×12×6+$\frac{1}{2}π$×62=18π+36，
    锥体的高h=$\sqrt{{12}^{2}-{6}^{2}}$=6$\sqrt{3}$，
    故锥体的体积V=$\frac{1}{3}Sh$=36$\sqrt{3}$（π+2），
    故答案为：36$\sqrt{3}$（π+2）

    点评 本题考查的知识点是由三视图求体积和表面积，解决本题的关键是得到该几何体的形状．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    2．已知抛物线y2=12x焦点的一条直线与抛物线相交于A、B两点，若|AB|=10，则线段AB的中点到y轴的距离等于（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．在O点测量到远处有一物体在做匀速直线运动，开始时该物体位于P点，一分钟后，其位置在Q点，且∠POQ=90°，再过两分钟后，该物体位于R点，且∠QOR=30°，则tan∠OPQ的值为$\frac{2\sqrt{3}}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．设a，b∈R，则a2（a-b）＞0是a＞b的（　　）
    A．充分不必要条件B．必要不充分条件
    C．充要条件D．既不必要也不充分条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．判断下列函数的奇偶性．
    （1）f（x）=x2-x3．
    （2）f（x）=$\sqrt{{x}^{2}-1}$+$\sqrt{1-{x}^{2}}$
    （3）f（x）=$\frac{\sqrt{4-{x}^{2}}}{|x+3|-3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．已知函数f（x）=-x2+mx-n，m，n是区间[0，3]内任意两个实数，则事件f（1）＜0发生的概率为$\frac{7}{9}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．已知△ABC中，内角A，B，C所对的边长分别为a，b，c．若a=2bcosA，B=$\frac{π}{3}$，c=1，则△ABC的面积等于（　　）
    A．$\frac{{\sqrt{3}}}{8}$B．$\frac{{\sqrt{3}}}{6}$C．$\frac{{\sqrt{3}}}{4}$D．$\frac{{\sqrt{3}}}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．在平面直角坐标系中，把横、纵坐标均为有理数的点称为有理点．若a为无理数，则在过点P（a，-$\frac{1}{2}$）的所有直线中（　　）
    A．有无穷多条直线，每条直线上至少存在两个有理点
    B．恰有n（n≥2）条直线，每条直线上至少存在两个有理点
    C．有且仅有一条直线至少过两个有理点
    D．每条直线至多过一个有理点

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．下列四个命题中正确命题的是（　　）
    A．学校抽取每个班级座号为21-30号的同学检查作业完成情况，这是分层抽样
    B．可以通过频率分布直方图中最高小矩形的高来估计这组数据的众数
    C．设随机变量ξ服从正态分布N（0，1），若P（ξ＞1）=p，则P（-1＜ξ＜0）=1-p
    D．在散点图中，回归直线至少经过一个点

    查看答案和解析>>

    同步练习册答案