
分析 (1)由题意:图象与x轴的交点,相邻两个交点之间的距离为$\frac{π}{4}$,可得周期为$\frac{π}{2}$,可求得ω,图象过点M($\frac{π}{3},-1}$)带入可求得φ,即可得到解析式.
(2)根据正弦函数的图象及性质即可求单调递增区间.
(3)根据三角函数平移变换的规律,求解g(x),在[0,$\frac{π}{2}}$]上求解g(x)的图象.g(x)+k=0有且只有一个实数解,即图象g(x)与y=-k,只有一个交点,即可求实数k的取值范围.
解答 解:(1)由题意:图象与x轴的交点,相邻两个交点之间的距离为$\frac{π}{4}$,即$\frac{1}{2}T=\frac{π}{4}$,即T=$\frac{π}{2}$;
∵T=$\frac{π}{2}=\frac{2π}{ω}$,解得:ω=4,那么:f(x)=sin(4x+φ).
∵0<φ<$\frac{π}{2}}$.图象过点M($\frac{π}{3},-1}$)带入可求得φ=$\frac{π}{6}$,
∴解析式$f(x)=sin({4x+\frac{π}{6}})$;
(2)由正弦函数的性质可知:$4x+\frac{π}{6}$∈[2kπ$-\frac{π}{2}$,2kπ$+\frac{π}{2}$],(k∈Z)是单调递增区间,即:2kπ$-\frac{π}{2}$≤$4x+\frac{π}{6}$≤2kπ$+\frac{π}{2}$],解得:$\frac{1}{2}$kπ-$\frac{π}{6}$≤x≤$\frac{1}{2}$kπ$+\frac{π}{12}$],(k∈Z)
∴函数f(x)的单调递增区间为:$[{-\frac{π}{6}+\frac{kπ}{2},\frac{π}{12}+\frac{kπ}{2}}],k∈Z$;
(3)由(1)可知:$f(x)=sin({4x+\frac{π}{6}})$;将f(x)的图象向右平移$\frac{π}{8}$个单位后,得到$y=sin({4x-\frac{π}{3}})$的图象,
再将所得图象所有点的横坐标伸长到原来的2倍(纵坐标不变),得到$y=sin({2x-\frac{π}{3}})$的图象.即g(x)=sin(2x-$\frac{π}{3}$)
∵$0≤x≤\frac{π}{2}$
∴$-\frac{π}{3}$≤2x-$\frac{π}{3}$≤$\frac{2π}{3}$
g(x)+k=0在[0,$\frac{π}{2}}$]上只有一个实数解,即图象g(x)与y=-k,只有一个交点,
当x=$-\frac{π}{3}$时,g(x)图象取得最低点,即g(-$\frac{π}{3}$)=$-\frac{\sqrt{3}}{2}$.由正弦函数图象可知:$-\frac{{\sqrt{3}}}{2}<k≤\frac{{\sqrt{3}}}{2}$时只有一个交点,以及k=-1时,也有一个交点.即实数k的取值范围为:$-\frac{{\sqrt{3}}}{2}<k≤\frac{{\sqrt{3}}}{2}$或k=-1.
点评 本题考查了三角函数图象及性质的运用能力和化简能力,平移变换的规律,数形结合法的应用.综合性强,属于难题.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
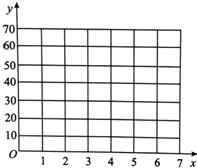 为了探究车流量与PM2.5的浓度是否相关,现采集到北方某城市2015年12月份星期一到星期日某一时间段车流量与PM2.5的数据如表:
为了探究车流量与PM2.5的浓度是否相关,现采集到北方某城市2015年12月份星期一到星期日某一时间段车流量与PM2.5的数据如表:| 时间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 |
| 车流量x(万辆) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| PM2.5的浓度y (微克/立方米) | 27 | 31 | 35 | 41 | 49 | 56 | 62 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
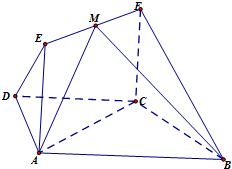 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com