
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
已知△ABC的内角A,B,C所对的边分别为a,b,c,且a=2,cosB=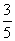 .
.
(Ⅰ)若b=4,求sinA的值;
(Ⅱ)若△ABC的面积S△ABC=4,求b,c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
某商场举行抽奖活动,从装有编为0,1,2,3四个小球的抽奖箱中同时抽出两个小球,两个小球号码之和等于5中一等奖,等于4中二等奖,等于3中三等奖.
(Ⅰ)求中三等奖的概率;
(Ⅱ)求中奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
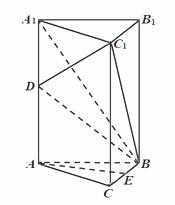
如图,在正三棱柱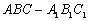 中,已知
中,已知 ,
,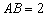 ,
,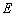 是
是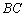 的中点,
的中点, 在棱
在棱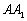 上.
上.
(I)求异面直线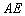 与
与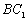 所成角;
所成角;
(II)若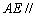 平面
平面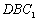 ,求
,求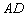 长;
长;
(III)在棱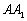 上是否存在点
上是否存在点 ,使得二面角
,使得二面角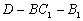 的大小等于
的大小等于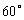 ,若存在,求
,若存在,求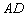 的长;若不存在,说明理由.
的长;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图是一几何体的平面展开图,其中ABCD为正方形,E,F分别为PA,PD的中点.在此几何体中,给出下面四个结论:
①B,E,F,C四点共面; ②直线BF与AE异面;
③直线EF∥平面PBC; ④平面BCE⊥平面PAD;.
⑤折线B→E→F→C是从B点出发,绕过三角形PAD面,到达点C的一条最短路径.
其中正确的有_____________.(请写出所有符合条件的序号)

查看答案和解析>>
科目:高中数学 来源: 题型:
已知 ,过点
,过点 作一直线与双曲线
作一直线与双曲线 相交且仅有一个公共点,则该直线的倾斜角恰好等于此双曲线渐近线的倾斜角
相交且仅有一个公共点,则该直线的倾斜角恰好等于此双曲线渐近线的倾斜角 或
或 ;类比此思想,已知
;类比此思想,已知 ,过点
,过点 作一直线函数
作一直线函数 的图象相交且仅有一个公共点,则该直线的倾斜角为 .
的图象相交且仅有一个公共点,则该直线的倾斜角为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com