
| A. | $\sqrt{3}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | 0 | D. | -$\frac{{\sqrt{3}}}{2}$ |
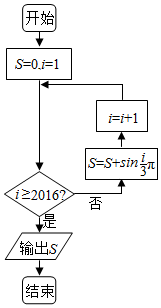
分析 模拟程序框图的运行过程,得出该程序运行后输出的算式S,利用正弦函数的周期性求出S的值即可.
解答 解:模拟程序框图的运行过程,得;
该程序运行后输出的是
S=sin$\frac{π}{3}$+sin$\frac{2π}{3}$+sin$\frac{3π}{3}$+sin$\frac{4π}{3}$+sin$\frac{5π}{3}$+…+sin$\frac{iπ}{3}$;
分析最后一次循环情况,i=2015时,不满足条件i≥2016,执行循环:
S=sin$\frac{π}{3}$+sin$\frac{2π}{3}$+sin$\frac{3π}{3}$+sin$\frac{4π}{3}$+sin$\frac{5π}{3}$+…+sin$\frac{2015π}{3}$
=[sin$\frac{π}{3}$+sin$\frac{2π}{3}$+sin$\frac{3π}{3}$+sin$\frac{4π}{3}$+sin$\frac{5π}{3}$+sin$\frac{6π}{3}$]+…
+[sin(670π+$\frac{π}{3}$)+sin(670π+$\frac{2π}{3}$)+sin(sin670π+$\frac{3π}{3}$)+sin(670π+$\frac{4π}{3}$)+sin(670π+$\frac{5π}{3}$)]
=[$\frac{\sqrt{3}}{2}$+$\frac{\sqrt{3}}{2}$+0+(-$\frac{\sqrt{3}}{2}$)+(-$\frac{\sqrt{3}}{2}$)+0]+…+[$\frac{\sqrt{3}}{2}$+$\frac{\sqrt{3}}{2}$+0+(-$\frac{\sqrt{3}}{2}$)+(-$\frac{\sqrt{3}}{2}$)]
=0,
i=2016时,满足条件i≥2016,退出循环,输出S=0.
故选:C.
点评 本题考查了程序框图的应用问题,也考查了正弦函数的周期性问题,是基础题目.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.45 | B. | 0.05 | C. | 0.4 | D. | 0.6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
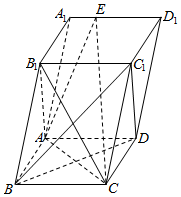 如图,斜四棱柱ABCD-A1B1C1D1的底面是边长为1的正方形,侧面AA1B1B⊥底面ABCD,AA1=2,∠B1BA=60°.
如图,斜四棱柱ABCD-A1B1C1D1的底面是边长为1的正方形,侧面AA1B1B⊥底面ABCD,AA1=2,∠B1BA=60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
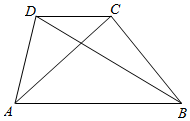 如图,在梯形ABCD中,AB∥CD,AD=6,cos∠ADC=-$\frac{1}{3}$.
如图,在梯形ABCD中,AB∥CD,AD=6,cos∠ADC=-$\frac{1}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
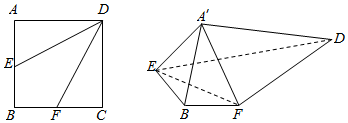
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com