
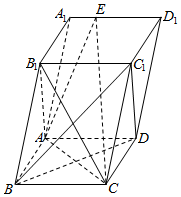
 如图,斜四棱柱ABCD-A1B1C1D1的底面是边长为1的正方形,侧面AA1B1B⊥底面ABCD,AA1=2,∠B1BA=60°.
如图,斜四棱柱ABCD-A1B1C1D1的底面是边长为1的正方形,侧面AA1B1B⊥底面ABCD,AA1=2,∠B1BA=60°.分析 (Ⅰ)由已知利用余弦定理求出$A{{B}_{1}}^{2}$,从而利用勾股定理得到B1A⊥AB,由侧面AA1B1B⊥底面ABCD,得B1A⊥BD,由ABCD是正方形,得AC⊥BD,从而BD⊥平面AB1C,由此能证明平面AB1C⊥平面BDC1.
(Ⅱ)以AB、AD、AB1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,由向量法能求出在棱A1D1上存在点E,使二面角E-AC-B1的余弦值是$\frac{\sqrt{6}}{3}$,$\frac{{A}_{1}E}{{A}_{1}{D}_{1}}$=$\sqrt{3}-1$.
解答 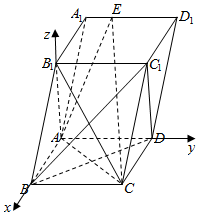 (Ⅰ)证明:∵$A{{B}_{1}}^{2}$=$A{B}^{2}+B{{B}_{1}}^{2}-2AB•B{B}_{1}•cos60°$=3,
(Ⅰ)证明:∵$A{{B}_{1}}^{2}$=$A{B}^{2}+B{{B}_{1}}^{2}-2AB•B{B}_{1}•cos60°$=3,
∴$A{{B}_{1}}^{2}+A{B}^{2}=B{{B}_{1}}^{2}$,
∴B1A⊥AB,又∵侧面AA1B1B⊥底面ABCD,
∴B1A⊥底面ABCD,∴B1A⊥BD,…(3分)
又∵ABCD是正方形,∴AC⊥BD,∴BD⊥平面AB1C,
∴平面AB1C⊥平面BDC1.…(5分)
解:(Ⅱ)由(Ⅰ)知B1A⊥AB,B1A⊥AD,
如图以AB、AD、AB1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,
则A(0,0,0),B(1,0,0),C(1,1,0),D(0,1,0),B1(0,0,$\sqrt{3}$),
平面AB1C的法向量为$\overrightarrow{BD}$=(-1,1,0),
设$\overrightarrow{{A}_{1}E}$=λ$\overrightarrow{{A}_{1}{D}_{1}}$,平面ACE的法向量$\overrightarrow{m}$=(x,y,z),
则$\overrightarrow{{A}_{1}E}$=$λ\overrightarrow{AD}$=(0,λ,0),
$\overrightarrow{AE}$=$\overrightarrow{A{A}_{1}}$+$\overrightarrow{{A}_{1}E}$=$\overrightarrow{B{B}_{1}}+\overrightarrow{{A}_{1}E}$=(-1,λ,$\sqrt{3}$),
由$\overrightarrow{m}•\overrightarrow{AE}$=0,得-x+$λy+\sqrt{3}z$=0,
由$\overrightarrow{m}•\overrightarrow{AC}$=0,得x+y=0,令x=1,则y=-1,z=$\frac{λ+1}{\sqrt{3}}$,
即$\overrightarrow{m}$=(1,-1,$\frac{λ+1}{\sqrt{3}}$),…(8分)
∴cos<$\overrightarrow{BD},\overrightarrow{m}$>=$\frac{-2}{\sqrt{2}•\sqrt{2+\frac{(λ+1)^{2}}{3}}}$,
∴$\frac{2}{\sqrt{2}•\sqrt{2+\frac{(λ+1)^{2}}{3}}}$=$\frac{\sqrt{6}}{3}$,解得$λ=\sqrt{3}-1$,
∴在棱A1D1上存在点E,使二面角E-AC-B1的余弦值是$\frac{\sqrt{6}}{3}$,$\frac{{A}_{1}E}{{A}_{1}{D}_{1}}$=$\sqrt{3}-1$.…(12分)
点评 本题考查面面垂直的证明,考查满足条件的点是否存在的判断与求法,是中档题,解题时要认真审题,注意向量法的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | 0 | D. | -$\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 48种 | B. | 72种 | C. | 144种 | D. | 288种 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,$\frac{1}{3}$] | B. | (2,+∞) | C. | (-∞,$\frac{1}{2}$] | D. | D[$\frac{1}{2}$,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | -$\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | -$\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 抛掷一颗均匀的骰子,出现点数是2 | |
| B. | 抛掷一颗均匀的骰子,出现点数是4 | |
| C. | 抛掷一颗均匀的骰子,出现点数是6 | |
| D. | 抛掷一颗均匀的骰子,出现点数是偶数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
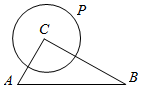 如图,直角三角形ACB的斜边AB=2$\sqrt{3}$,∠ABC=$\frac{π}{6}$,点P是以点C为圆心1为半径的圆上的动点.
如图,直角三角形ACB的斜边AB=2$\sqrt{3}$,∠ABC=$\frac{π}{6}$,点P是以点C为圆心1为半径的圆上的动点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com