练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    1．点$（{\sqrt{3}，4}）$在直线l：ax-y+1=0上，则直线l的倾斜角为（　　）
    A．30°B．45°C．60°D．120°

    分析 点$（{\sqrt{3}，4}）$在直线l：ax-y+1=0上，a=$\sqrt{3}$，即直线的斜率为$\sqrt{3}$可得直线的倾斜角．

    解答 解：∵点$（{\sqrt{3}，4}）$在直线l：ax-y+1=0上，
    ∴$\sqrt{3}a-4+1=0$，
    ∴a=$\sqrt{3}$，即直线的斜率为$\sqrt{3}$，直线l的倾斜角为60°．
    故选C．

    点评 本题考查直线的倾斜角，考查学生的计算能力，比较基础．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    11．结合下面的算法：
    第一步，输入x．
    第二步，若x＜0，则y=x+3；否则，y=x-1．
    第三步，输出y．
    当输入的x的值为3时，输出的结果为2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．在△ABC中，角A，B，C的对边分别为a，b，c，已知cosC+cosAcosB=2cosAsinB．
    （1）求tanA；
    （2）若$b=2\sqrt{5}$，AB边上的中线$CD=\sqrt{17}$，求△ABC的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．若$2sin（{θ+\frac{π}{3}}）=3sin（{\frac{π}{3}-θ}）$，则tanθ=（　　）
    A．$-\frac{{\sqrt{3}}}{2}$B．$\frac{{\sqrt{3}}}{5}$C．$\frac{{2\sqrt{3}}}{3}$D．$2\sqrt{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

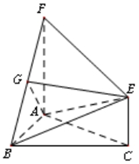    16．如图，三角形ABC和梯形ACEF所在的平面互相垂直，AB⊥BC，AF⊥AC，AF∥CE且AF=2CE，G是线段BF上一点，AB=AF=BC=2．
    （Ⅰ）当GB=GF时，求证：EG∥平面ABC；
    （Ⅱ）求二面角E-BF-A的余弦值；
    （Ⅲ）是否存在点G，满足BF⊥平面AEG？并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．点F1、F2分别是双曲线${x^2}-\frac{y^2}{3}=1$的左、右焦点，点P在双曲线上，则△PF1F2的内切圆半径r的取值范围是（　　）
    A．$（{0，\sqrt{3}}）$B．（0，2）C．$（{0，\sqrt{2}}）$D．（0，1）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

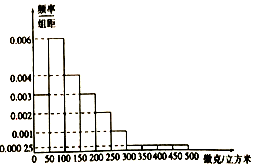    13．根据环境保护部《环境空气质量指数（AQI）技术规定》，空气质量指数（AQI）在201-300之间为重度污染；在301-500之间为严重污染．依据空气质量预报，同时综合考虑空气污染程度和持续时间，将空气重污染分4个预警级别，由轻到重依次为预警四级、预警三级、预警二级、预警一级，分别用蓝、黄、橙、红颜色标示，预警一级（红色）为最高级别．（一）预警四级（蓝色）：预测未来1天出现重度污染；（二）预警三级（黄色）：预测未来1天出现严重污染或持续3天出现重度污染；（三）预警二级（橙色）；预测未来持续3天交替出现重度污染或严重污染；（四）预警一级（红色）；预测未来持续3天出现严重污染．
    某城市空气质量监测部门对近300天空气中PM2.5浓度进行统计，得出这300天PM2.5浓度的频率分布直方图如图，将PM2.5浓度落入各组的频率视为概率，并假设每天的PM2.5浓度相互独立．
    （1）求当地监测部门发布颜色预警的概率；
    （2）据当地监测站数据显示未来4天将出现3天严重污染，求监测部门发布红色预警的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知圆C的方程为x2+y2=4，点P是圆C上任意一动点，过点P作x轴的垂线，垂足为H，且$\overrightarrow{OQ}$=$\frac{1}{2}$（$\overrightarrow{OP}$+$\overrightarrow{OH}$），动点Q的轨迹为E．轨迹E与x轴、y轴的正半轴分别交于点A和点B；直线y=kx（k＞0）与直线AB相交于点D，与轨迹E相交于M、N两点．
    （Ⅰ）求轨迹E的方程；
    （Ⅱ）求四边形AMBN面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．已知a，b，c∈（0，+∞），则下列三个数$a+\frac{4}{b}$，$b+\frac{9}{c}$，$c+\frac{16}{a}$（　　）
    A．都大于6B．至少有一个不大于6
    C．都小于6D．至少有一个不小于6

    查看答案和解析>>

    同步练习册答案