
| A. | $({0,\sqrt{3}})$ | B. | (0,2) | C. | $({0,\sqrt{2}})$ | D. | (0,1) |
分析 根据题意,利用切线长定理,再利用双曲线的定义,把|PF1|-|PF2|=2,转化为|HF1|-|HF2|=2,从而求得点H的横坐标,确定0°<∠IF1H<30°,即可求出△PF1F2的内切圆半径的取值范围.
解答 解:如图所示:F1(-2,0)、F2(2,0),
设内切圆与x轴的切点是点H,
PF1、PF2与内切圆的切点分别为M、N,
∵由双曲线的定义可得|PF1|-|PF2|=2,
由圆的切线长定理知,|PM|=|PN|,故|MF1|-|NF2 |=2,
即|HF1|-|HF2|=2,
设内切圆的圆心I横坐标为x,内切圆半径r,则点H的横坐标为x,
故 (x+c)-(c-x)=2,∴x=1,
∵双曲线${x^2}-\frac{y^2}{3}=1$的渐近线的方程为y=±$\sqrt{3}$x,
∴0°<∠PF1H<60°,
∴0°<∠IF1H<30°,
∴0<$\frac{r}{3}$<$\frac{\sqrt{3}}{3}$,
∴0<r<$\sqrt{3}$.
△PF1F2的内切圆半径r的取值范围(0,$\sqrt{3}$),
故选A.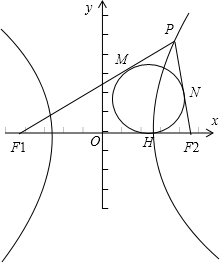
点评 本题考查双曲线的定义、切线长定理,体现了转化的数学思想以及数形结合的数学思想,正确运用双曲线的定义是关键,属于中档题.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}}}{10}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{{\sqrt{10}}}{5}$ | D. | $\frac{{\sqrt{10}}}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
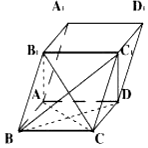 如图,斜四棱柱ABCD-A1B1C1D1的底面是边长为$\sqrt{3}$的正方形,侧面A1ABB1⊥底面ABCD,AA1=2,∠B1BA=30°.
如图,斜四棱柱ABCD-A1B1C1D1的底面是边长为$\sqrt{3}$的正方形,侧面A1ABB1⊥底面ABCD,AA1=2,∠B1BA=30°.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com