
(12分)某高校在2012年的自主招生考试中随机抽取了100名学生的笔试成绩,按成绩分组:第一组[160,165),第二组[165,170),第三组[170,175),第四组[175,180),第五组[180,185)得到的频率分布直方图如图所示.
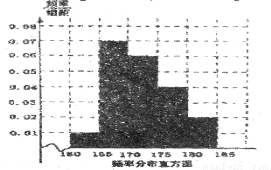
(1)求第三、四、五组的频率;
(2)为了以选拔出最优秀的学生,学校决定在笔试成绩高的第三、四、五组中用分层抽样抽取6名学生进入第二轮面试,求第三、四、五组每组各抽取多少名学生进入第二轮面试.
(3)在(2)的前提下,学校决定在这6名学生中随机抽取2名学生接受甲考官的面试,求第四组至少有一名学生被甲考官面试的概率.
(1)0.3,0.2,0.1;(2)3人,2人,1人;(3)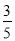
【解析】
试题分析:(1)如频率分布直方图可知,小正方形的面积为频率,根据所给的数据可得到第三、四、五组的频率.
(2)根据频率分布直方图可求出第三、四、五组的人数,即可得每组占这三组人数和的百分比,由分层抽样抽的实验方法,即可得每组所取得人数.
(3)由6名学生中抽取两名学生共有15种情况,由于第四组有两名学生.至少有一名被抽到的情况包括两种情况,只有一个被抽到和两个都被抽到.共9种情况.即可得结论.
试题解析:(1)由题设可知,第三组的频率为0.06×5=0.3第四组的频率为0.04×5=0.2第五组的频率为0.02×5=0.1
(2)第三组的人数为0.3×100=30 第四组的人数为0.2×100=20第五组的人数为0.1×100=10因为第三、四、五组共有60名学生,所以利用分层抽样在60名学生中抽取6名学生,每组抽到的人数分别为:第三组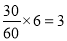 第四组
第四组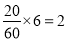 第五组
第五组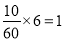 ,所以第三、四、五组分别抽取3人,2人,1人.
,所以第三、四、五组分别抽取3人,2人,1人.
(3)设第三组的3位同学为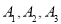 ,第四组的2为同学为
,第四组的2为同学为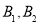 ,第五组的1为同学为C1,则从6为同学中抽2位同学有:
,第五组的1为同学为C1,则从6为同学中抽2位同学有: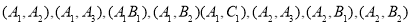
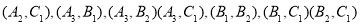 共15种可能其中第四组的2为同学
共15种可能其中第四组的2为同学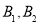 中至少1为同学入选有
中至少1为同学入选有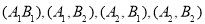 ,
,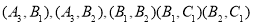 共9种可能。
共9种可能。
所以第四组至少有1位同学被甲考官面试的概率为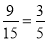 .
.
考点:1.统计概率问题.2.分层抽样.3.列举法.
考点分析: 考点1:古典概率 试题属性

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源:2014-2015学年安徽省马鞍山市高二上学期期末考试理科数学试卷(解析版) 题型:解答题
(本小题满分12分) 已知曲线 :
:  ,求曲线
,求曲线 在
在 轴上的所截的线段的长度为1的充要条件,证明你的结论.
轴上的所截的线段的长度为1的充要条件,证明你的结论.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年陕西省宝鸡市九校高三联合检测理科数学试卷(解析版) 题型:解答题
(本题满分10分)选修4—4:坐标系与参数方程.
坐标系与参数方程在直角坐标系xOy中,圆C的参数方程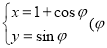 为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
(Ⅰ)求圆C的极坐标方程;
(Ⅱ)射线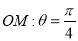 与圆C的交点为O、P两点,求P点的极坐标.
与圆C的交点为O、P两点,求P点的极坐标.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年陕西省宝鸡市九校高三联合检测理科数学试卷(解析版) 题型:选择题
一个四面体的顶点在空间直角坐标系 中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的主视图时,以
中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的主视图时,以 平面为投影面,则得到主视图可以为( )
平面为投影面,则得到主视图可以为( )

查看答案和解析>>
科目:高中数学 来源:2014-2015学年江西省吉安市高三上学期第二次阶段考试文科数学试卷(解析版) 题型:解答题
选修4—4:坐标系与参数方程
已知曲线C1的参数方程为 (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为 .
.
(Ⅰ)把C1的参数方程化为极坐标方程;(Ⅱ)求C1与C2交点的极坐标( ).
).
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江西省吉安市高三上学期第二次阶段考试文科数学试卷(解析版) 题型:选择题
设在△ABC中, ,
,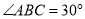 , AD是边BC上的高,则
, AD是边BC上的高,则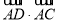 的值等于( )
的值等于( )
A.0 B.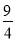 C.4 D.
C.4 D.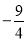
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河北省唐山市高三第一次模拟考试理科数学试卷(解析版) 题型:解答题
(本小题满分12分)已知圆 ,点
,点 ,以线段AB为直径的圆内切于圆
,以线段AB为直径的圆内切于圆 ,记点B的轨迹为
,记点B的轨迹为 .
.

(Ⅰ)求曲线 的方程;
的方程;
(Ⅱ)直线AB交圆 于C,D两点,当B为CD中点时,求直线AB的方程.
于C,D两点,当B为CD中点时,求直线AB的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com