
【题目】已知函数![]() 是定义在R上的奇函数,当
是定义在R上的奇函数,当![]() 时,
时,![]() ,则下列命题正确的是( )
,则下列命题正确的是( )
A.当![]() 时,
时,![]()
B.函数![]() 有3个零点
有3个零点
C.![]() 的解集为
的解集为![]()
D.![]() ,都有
,都有![]()
【答案】BCD
【解析】
设![]() ,则
,则![]() ,则由题意得
,则由题意得![]() ,根据奇函数
,根据奇函数![]() 即可求出解析式,即可判断A选项,再根据解析式分类讨论即可判断B、C两个选项,对函数求导,得单调性,从而求出值域,进而判断D选项.
即可求出解析式,即可判断A选项,再根据解析式分类讨论即可判断B、C两个选项,对函数求导,得单调性,从而求出值域,进而判断D选项.
解:(1)当![]() 时,
时,![]() ,则由题意得
,则由题意得![]() ,
,
∵ 函数![]() 是奇函数,
是奇函数,
∴ ![]() ,且
,且![]() 时,
时,![]()
![]()
![]() ,A错;
,A错;
∴ 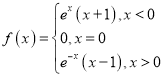 ,
,
(2)当![]() 时,由
时,由![]() 得
得![]() ,
,
当![]() 时,由
时,由![]() 得
得![]() ,
,
∴ 函数![]() 有3个零点
有3个零点![]() ,B对;
,B对;
(3)当![]() 时,由
时,由![]() 得
得![]() ,
,
当![]() 时,由
时,由![]() 得
得![]() ,
,
∴ ![]() 的解集为
的解集为![]() ,C对;
,C对;
(4)当![]() 时,由
时,由![]() 得
得![]() ,
,
由![]() 得
得![]() ,由
,由![]() 得
得![]() ,
,
∴ 函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
∴函数在![]() 上有最小值
上有最小值![]() ,且
,且![]()
![]() ,
,
又∵ 当![]() 时,
时,![]() 时
时![]() ,函数在
,函数在![]() 上只有一个零点,
上只有一个零点,
∴当![]() 时,函数
时,函数![]() 的值域为
的值域为![]() ,
,
由奇函数的图象关于原点对称得函数![]() 在
在![]() 的值域为
的值域为![]()
![]() ,
,
∴ 对![]() ,都有
,都有![]() ,D对;
,D对;
故选:BCD.


科目:高中数学 来源: 题型:
【题目】某地区2007年至2011年农村居民家庭纯收入y(单位:千元)的数据如下表:
年份 | 2007 | 2008 | 2009 | 2010 | 2011 |
年份代号t | 1 | 2 | 3 | 4 | 5 |
人均纯收入y | 3.1 | 3.6 | 3.9 | 4.4 | 5 |
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,分析2007年至2011年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为: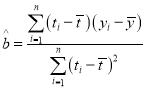 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为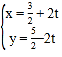 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系.曲线
轴正半轴为极轴建立极坐标系.曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程,曲线
的普通方程,曲线![]() 的参数方程;
的参数方程;
(2)若![]() 分别为曲线
分别为曲线![]() ,
,![]() 上的动点,求
上的动点,求![]() 的最小值,并求
的最小值,并求![]() 取得最小值时,
取得最小值时,![]() 点的直角坐标.
点的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在坐标原点,左右焦点分别为
的中心在坐标原点,左右焦点分别为![]() 和
和![]() ,且椭圆
,且椭圆![]() 经过点
经过点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过椭圆的右顶点![]() 作两条相互垂直的直线
作两条相互垂直的直线![]() ,
,![]() ,分别与椭圆交于点
,分别与椭圆交于点![]() (均异于点
(均异于点![]() ),求证:直线
),求证:直线![]() 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图为我国数学家赵爽(约3世纪初)在为《周髀算经》作注时验证勾股定理的示意图,现在提供5种颜色给其中5个小区域涂色,规定每个区域只涂一种颜色,相邻区域颜色不相同,则不同的涂色方案共有( )
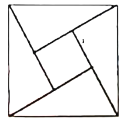
A.360种B.720种C.480种D.420种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“勾股定理”在西方被称为“毕达哥拉斯定理”,三国时期吴国的数学家赵爽创制了一幅“勾股圆方图”,用数形结合的方法给出了勾股定理的详细证明.如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个大正方形,若直角三角形的直角边的边长分别是3和4,在绘图内随机取一点,则此点取自小正方形的概率为( )
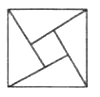
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某医药公司研发一种新的保健产品,从一批产品中抽取200盒作为样本,测量产品的一项质量指标值,该指标值越高越好.由测量结果得到如下频率分布直方图:
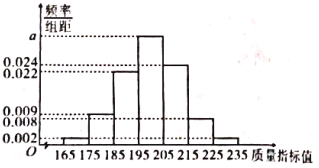
(Ⅰ)求![]() ,并试估计这200盒产品的该项指标的平均值;
,并试估计这200盒产品的该项指标的平均值;
(Ⅱ)① 用样本估计总体,由频率分布直方图认为产品的质量指标值![]() 服从正态分布
服从正态分布![]() ,计算该批产品指标值落在
,计算该批产品指标值落在![]() 上的概率;参考数据:附:若
上的概率;参考数据:附:若![]() ,则
,则![]() ,
,![]() .
.
②国家有关部门规定每盒产品该项指标不低150均为合格,且按指标值的从低到高依次分为:合格、优良、优秀三个等级,其中![]() 为优良,不高于180为合格,不低于220为优秀,在①的条件下,设公司生产该产品1万盒的成本为15万元,市场上每盒该产品的等级售价(单位:元)如图表,求该公司每万盒的平均利润.
为优良,不高于180为合格,不低于220为优秀,在①的条件下,设公司生产该产品1万盒的成本为15万元,市场上每盒该产品的等级售价(单位:元)如图表,求该公司每万盒的平均利润.
等级 | 合格 | 优良 | 优秀 |
价格 | 10 | 20 | 30 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有9名学生在同一间教室参加一次数学竞赛,座位排列成3行3列,用![]() 的方格棋盘表示,其中,每个方格代表一个座位为了避免舞弊,采用A、B、C三种类型的试卷,要使任何两个相邻的座位(有公共边的两个方格)发放的试卷类型不同.则符合条件的发放试卷的方法共有________种.
的方格棋盘表示,其中,每个方格代表一个座位为了避免舞弊,采用A、B、C三种类型的试卷,要使任何两个相邻的座位(有公共边的两个方格)发放的试卷类型不同.则符合条件的发放试卷的方法共有________种.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com