
【题目】已知函数f(x)= ![]() .
.
(1)判断f(x)在(0,+∞)的单调性;
(2)若x>0,证明:(ex﹣1)ln(x+1)>x2 .
【答案】
(1)解:由函数f(x)的定义域为(﹣1,0)∪(0,+∞)
∴f′(x)= ![]() ,
,
设g(x)= ![]() ﹣ln(1+x),
﹣ln(1+x),
∴g′(x)= ![]() ﹣
﹣ ![]() =
= ![]() <0,
<0,
∴g(x)在(0,+∞)为减函数,
∴g(x)<g(0)=0,
∴f′(x)<0,
∴f(x)在(0,+∞)为减函数
(2)解:(ex﹣1)ln(x+1)>x2等价于 ![]() >
> ![]() ,
,
∵ ![]() =
= ![]() =
= ![]() ,
,
∴原不等式等价于 ![]() >
> ![]() ,
,
由(1)知,f(x)= ![]() 是(0,+∞)上的减函数,
是(0,+∞)上的减函数,
∴要证原不等式成立,只需要证明当x>0时,x<ex﹣1,
令h(x)=ex﹣x﹣1,
∴h′(x)=ex﹣1>0,
∴h(x)是(0,+∞)上的增函数,
∴h(x)>h(0)=0,
即x<ex﹣1,
∴f(x)>f(ex﹣1),
即 ![]() >
> ![]() =>
=> ![]() ,
,
故(ex﹣1)ln(x+1)>x2
【解析】(1)根据导数和函数单调性的关系,以及导数和最值得关系即可求出;(2)原不等式等价于 ![]() >
> ![]() ,要证原不等式成立,只需要证明当x>0时,x<ex﹣1,令h(x)=ex﹣x﹣1,利用导数和最值得关系即可证明.
,要证原不等式成立,只需要证明当x>0时,x<ex﹣1,令h(x)=ex﹣x﹣1,利用导数和最值得关系即可证明.
【考点精析】通过灵活运用利用导数研究函数的单调性,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减即可以解答此题.
在这个区间单调递减即可以解答此题.


科目:高中数学 来源: 题型:
【题目】下列3个命题:
(1)函数f(x)在x>0时是增函数,x<0也是增函数,所以f(x)是增函数;
(2)若函数f(x)=ax2+bx+2与x轴没有交点,则b2﹣8a<0且a>0;
(3)y=x2﹣2|x|﹣3的递增区间为[1,+∞).
其中正确命题的个数是( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+2x+c(a、c∈N*)满足:①f(1)=5;②6<f(2)<11.
(1)求a、c的值;
(2)若对任意的实数x∈[ ![]() ,
, ![]() ],都有f(x)﹣2mx≤1成立,求实数m的取值范围.
],都有f(x)﹣2mx≤1成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年年底,某商业集团根据相关评分标准,对所属20家商业连锁店进行了年度考核评估,并依据考核评估得分(最低分60分,最高分100分)将这些连锁店分别评定为A,B,C,D四个类型,其考核评估标准如下表:
评估得分 | [60,70) | [70,80) | [80,90) | [90,100] |
评分类型 | D | C | B | A |
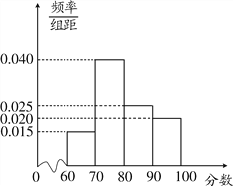 考核评估后,对各连锁店的评估分数进行统计分析,得其频率分布直方图如下:
考核评估后,对各连锁店的评估分数进行统计分析,得其频率分布直方图如下:
(Ⅰ)评分类型为A的商业连锁店有多少家;
(Ⅱ)现从评分类型为A,D的所有商业连锁店中随机抽取两家做分析,求这两家来自同一评分类型的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,从参加环保知识竞赛的学生中抽出40名,将其成绩(均为整数)整理后画出的频率分布直方图如下:

观察图形,回答下列问题:
(1)估计这次环保知识竞赛成绩的中位数;
(2)从成绩是80分以上(包括80分)的学生中选两人,求他们在同一分数段的概率?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型超市拟对店庆当天购物满![]() 元的顾客进行回馈奖励.规定:顾客转动十二等分且质地均匀的圆形转盘(如图),待转盘停止转动时,若指针指向扇形区域,则顾客可领取此区域对应面额(单位:元)的超市代金券.假设转盘每次转动的结果互不影响.
元的顾客进行回馈奖励.规定:顾客转动十二等分且质地均匀的圆形转盘(如图),待转盘停止转动时,若指针指向扇形区域,则顾客可领取此区域对应面额(单位:元)的超市代金券.假设转盘每次转动的结果互不影响.
(Ⅰ)若![]() ,求顾客转动一次转盘获得
,求顾客转动一次转盘获得![]() 元代金券的概率;
元代金券的概率;
(Ⅱ)某顾客可以连续转动两次转盘并获得相应奖励,当![]() 时,求该顾客第一次获得代金券的面额不低于第二次获得代金券的面额的概率;
时,求该顾客第一次获得代金券的面额不低于第二次获得代金券的面额的概率;
(Ⅲ)记顾客每次转动转盘获得代金券的面额为![]() ,当
,当![]() 取何值时,
取何值时, ![]() 的方差最小?
的方差最小?
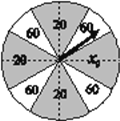
(结论不要求证明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com