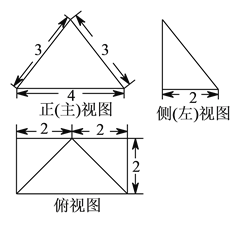
【题目】某四棱锥的三视图如图所示，该四棱锥的四个侧面的面积中最大的是（ ）．
A. 
B. 
C. 
D. 
【答案】C
【解析】由三视图得几何体是如图所示四棱锥
，
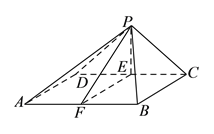
其中
， 
分别是
， 
中点， 
平面
，
底面
是矩形， 
， 
， 
是等腰三角形， 
，
∴
， 
，
∴
， 
，
．
∴四棱锥
的四个侧面中面积最大的是
．
故选
．
点睛:思考三视图还原空间几何体首先应深刻理解三视图之间的关系，遵循“长对正，高平齐，宽相等”的基本原则，其内涵为正视图的高是几何体的高，长是几何体的长；俯视图的长是几何体的长，宽是几何体的宽；侧视图的高是几何体的高，宽是几何体的宽.由三视图画出直观图的步骤和思考方法：1、首先看俯视图，根据俯视图画出几何体地面的直观图；2、观察正视图和侧视图找到几何体前、后、左、右的高度；3、画出整体，然后再根据三视图进行调整.
科目：高中数学 来源： 题型：
【题目】如图，在四棱锥
中，底面为等腰梯形，且底面与侧面
垂直， 
， 
分别为线段
的中点， 
， 
， 
，且
.
（1）证明： 
平面
；
（2）求
与平面
所成角的正弦值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知抛物线
的焦点为
抛物线
上存在一点
到焦点
的距离等于3.
（1）求抛物线
的方程；
（2）过点
的直线
与抛物线
相交于
两点（
两点在
轴上方），点
关于
轴的对称点为
，且
，求
的外接圆的方程.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，已知圆C1：x2+y2=4，圆C2：（x﹣2）2+y2=4．
（1）在以O为极点，x轴正半轴为极轴的极坐标系中，分别求圆C1与圆C2的极坐标方程及两圆交点的极坐标；
（2）求圆C1与圆C2的公共弦的参数方程．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某公司试销一种成本单价为500元的新产品，规定试销时销售单价不低于成本单价，又不高于800元．经试销调查，发现销售量y(件)与销售单价x(元)之间的关系可近似看作一次函数y＝kx＋b(k≠0)，函数图象如图所示．
(1)根据图象，求一次函数y＝kx＋b(k≠0)的表达式；
(2)设公司获得的毛利润(毛利润＝销售总价－成本总价)为S元．试问销售单价定为多少时，该公司可获得最大毛利润？最大毛利润是多少？此时的销售量是多少？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
