|
|
|
高和底面圆直径均为2的圆柱被沿平面ACD和平面BCD从顶部斜切掉两块,如图所示,CD和AB分别是圆柱上、下底面圆的直径,AB上CD,且四边形CDEF为正方形.
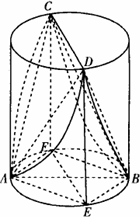
(Ⅰ)求证:平面ABD⊥平面CDEF;
(Ⅱ)求多面体CDAEBF的体积.
|
|
|
练习册系列答案
相关习题
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
若实数t满足f(t)=-t,则称t是函数f(x)的一个次不动点.设函数f(x)=lnx与函数g(x)=ex(其中e为自然对数的底数)的所有次不动点之和为m,则
|
| [ ] |
A. |
m<0
|
B. |
m=0
|
C. |
0<m<1
|
D. |
m>1
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
数列{an}共有11项,a1=0,a11=4,且|ak+1-ak|=1,k=1,2,3,……,10.满足这样条件的不同数列的个数为________;
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
定义在R上的函数f(x)满足下列三个条件:①对任意的x1,x2∈(-∞,0}(x1≠x2),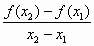 恒为正值;②f(-x)+f(x)=0;③f(x+y)=f(x)+f(y).则函数f(x)只可以是 恒为正值;②f(-x)+f(x)=0;③f(x+y)=f(x)+f(y).则函数f(x)只可以是
|
| [ ] |
A. |
f(x)=2x
|
B. |
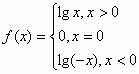
|
C. |
f(x)=3|x|
|
D. |
f(x)=x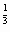
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
若函数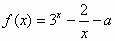 在区间(1,2)内存在零点,则实数a的取值范围是________. 在区间(1,2)内存在零点,则实数a的取值范围是________.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
在平面直角坐标系xOy中,已知圆锥曲线C的参数方程为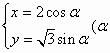 为参数). 为参数).
(Ⅰ)以原点为极点,x轴正半轴为极轴建立极坐标系,求圆锥曲线C的极坐标方程;
(Ⅱ)若直线l过曲线C的焦点且倾斜角为60°,求直线l被圆锥曲线C所截得的线段的长度.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
已知 那么( 那么( 展开式中含x2项的系数为 展开式中含x2项的系数为
|
| [ ] |
A. |
125
|
B. |
135
|
C. |
-135
|
D. |
-125
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
在平面直角坐标系xOy中,已知圆锥曲线C的参数方程为 为参数). 为参数).
(Ⅰ)以原点为极点,x轴正半轴为极轴建立极坐标系,求圆锥曲线C的极坐标方程;
(Ⅱ)若直线l过曲线C的焦点且倾斜角为60°,求直线l被圆锥曲线C所截得的线段的长度.
|
|
|
查看答案和解析>>
