
分析 分别指出集合A和集合B的元素的意义,再根据交集的定义即可求出答案.
解答 解:∵A={x|x=$\frac{n}{2}$,n∈Z}中的元素表示所有的整数被2除所的数,所得结果有整数,有整数加$\frac{1}{2}$,
或者为A={…,-$\frac{1}{2}$,0,$\frac{1}{2}$,1,$\frac{3}{2}$,2,…}
B={x|x=$\frac{n}{3}$,n∈Z},中的元素表示所有的整数被2除所的数,所得结果有整数,有整数加$\frac{1}{3}$或$\frac{2}{3}$,
或者为A={…,-$\frac{2}{3}$,-$\frac{1}{3}$,0,$\frac{1}{3}$,$\frac{2}{3}$,1,$\frac{4}{3}$,$\frac{5}{3}$,2,…}
∴A∩B={…,-3,-2,-1,0,1,2,…}=Z,
故答案为:Z
点评 本题考查了集合元素的意义和交集的运算,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 项目方式 | 基本费 | 网络使用费 | 通信费 |
| 963 | 0 | 0.05元/min | 0.02元/min |
| 169 | 100元/月 | 1元/h |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
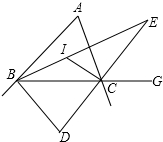 好学的小红在学完三角形的角平分线后,遇到下列4个问题,请你帮她解决,如图,在ABC中,∠BAC=50°,点I是两角B、C平分线的交点.
好学的小红在学完三角形的角平分线后,遇到下列4个问题,请你帮她解决,如图,在ABC中,∠BAC=50°,点I是两角B、C平分线的交点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com