Question

已知二次函数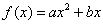满足条件 ：①对任意x∈R,均有 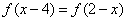②函数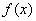的图像与y=x相切．

(1)求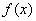的解析式；

(2) 若函数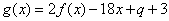，是否存在常数t (t≥0)，当x∈[t,10]时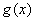，的值域为区间D，且D的长度为12－t，若存在，请求出t值，若不存在，请说明理由(注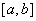： 的区间长度为)．

Answer 1

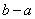解：(1)由①，a(x-4)^2+b(x-4)=a(2-x)^2+b(2-x),∴（2x-6)(-2a+b)=0,b=2a  2分由②，ax^2+(2a-1)x=0的两根相等，∴a=1/2,b=1. f(x)=(1/2)x^2+x.  4分所以g(x)＝x2－16x＋q＋3. (2)∵0≤t＜10，f(x)在区间[0,8]上是减函数，在区间[8,10]上是增函数，且其图象的对称轴是x＝8.①当0≤t≤6时，在区间[t,10]上，f(t)最大，f(8)最小，∴f(t)－f(8)＝12－t，即t²－15t＋52＝0，解得t＝，∴t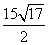＝；②当6＜t≤8时，在区间[t,10]上，f(10)最大，f(8)最小，∴f(10)－f(8)＝12－t，解得t＝8；③当8＜t＜10时，在区间[t,10]上，f(10)最大，f(t)最小，∴f(10)－f(t)＝12－t，即t²－17t＋72＝0，解得t＝8(舍去)或t＝9.综上可知，存在常数t为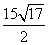，8,9满足题意．