
| A. | 直线a,b,c,若a∥b,b∥c,则a∥c,类推出:向量$\overrightarrow a$,$\overrightarrow b$,$\overrightarrow c$,若$\overrightarrow a$∥$\overrightarrow b$,$\overrightarrow b$∥$\overrightarrow c$,则$\overrightarrow a$∥$\overrightarrow c$ | |
| B. | 同一平面内,直线a,b,c,若a⊥c,b⊥c,则a∥b,类推出:空间中,直线a,b,c,若a⊥c,b⊥c,则a∥b | |
| C. | 实数a,b,若方程x2+ax+b=0有实数根,则a2≥4b,类推出:复数a,b,若方程x2+ax+b=0有实数根,则a2≥4b | |
| D. | 由向量加法的几何意义,可以类比得到复数加法的几何意义 |
分析 本题考查的知识点是类比推理,我们根据判断命题真假的办法,对四个答案中类比所得的结论逐一进行判断,即可得到答案.
解答 解:对于A,$\overrightarrow{b}$=$\overrightarrow{0}$时,不正确;
对于B,空间中,直线a,b,c,若a⊥c,b⊥c,则a∥b或a⊥b或相交,故不正确;
对于C,方程x02+ix0+(-1±i)=0有实根,但a2≥4b不成立,故C不正确;
对于D,由向量加法的几何意义可以类比得到复数加法的几何意义,正确.
故选:D.
点评 归纳推理与类比推理不一定正确,我们在进行类比推理时,一定要注意对结论进行进一步的论证,如果要证明一个结论是正确的,要经过严密的论证,但要证明一个结论是错误的,只需要举出一个反例.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
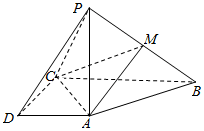 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,AD⊥CD,BC=2,AD=CD=1,M是PB的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,AD⊥CD,BC=2,AD=CD=1,M是PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
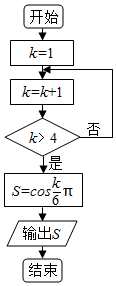
| A. | -$\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$或$\frac{3π}{4}$ | B. | $\frac{π}{3}$或$\frac{2π}{3}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com