
分析 (Ⅰ)利用函数是奇函数,结合f(0)=0,解方程即可求实数a的值;
(Ⅱ)结合方式函数的性质即可求函数f(x)的值域;
(Ⅲ)利用定义法判断函数的单调性,结合函数奇偶性和单调性的关系即可证明当m+n≠0时,比较$\frac{f(m)+f(n)}{{{m^3}+{n^3}}}$与f(0)的大小关系.
解答 解:(Ⅰ)∵函数$f(x)=a-\frac{1}{{{2^x}+1}}$在R上是奇函数,
∴f(0)=0,即$a-\frac{1}{{{2^0}+1}}=0$,
∴$a=\frac{1}{2}$;
(Ⅱ)由(Ⅰ)知$f(x)=\frac{1}{2}-\frac{1}{{{2^x}+1}}$,
∵2x+1>1,
∴0<$\frac{1}{{2}^{x}+1}$<1,
∴-1<-$\frac{1}{{2}^{x}+1}$<0,则$-\frac{1}{2}$<$\frac{1}{2}$-$\frac{1}{{2}^{x}+1}$<$\frac{1}{2}$,
即$-\frac{1}{2}<y<\frac{1}{2}$,
所以函数f(x)的值域为$(-\frac{1}{2},\frac{1}{2})$;
(Ⅲ)当m+n≠0时,$\frac{f(m)+f(n)}{{{m^3}+{n^3}}}>f(0)$.
设x1,x2∈R,且x1<x2,
$f({x_2})-f({x_1})=(\frac{1}{2}-\frac{1}{{{2^{x_2}}+1}})-(\frac{1}{2}-\frac{1}{{{2^{x_1}}+1}})=\frac{{{2^{x_2}}-{2^{x_1}}}}{{({2^{x_2}}+1)({2^{x_1}}+1)}}$
∵x1<x2,
∴${2^{x_2}}-{2^{x_1}}>0,({2^{x_2}}+1)({2^{x_1}}+1)>0$,
∴$\frac{{{2^{x_2}}-{2^{x_1}}}}{{({2^{x_2}}+1)({2^{x_1}}+1)}}>0$
即f(x2)-f(x1)>0,
所以函数$f(x)=\frac{1}{2}-\frac{1}{{{2^x}+1}}$在R上是单调递增,
①若m+n>0,即m>-n,所以f(m)>f(-n),m3>(-n)3,
又因为$f(x)=\frac{1}{2}-\frac{1}{{{2^x}+1}}$在R上是奇函数,
所以f(-n)=-f(n),f(m)+f(n)>0,m3+n3>0
所以$\frac{f(m)+f(n)}{{{m^3}+{n^3}}}>0$,
又因为f(0)=0,所以$\frac{f(m)+f(n)}{{{m^3}+{n^3}}}>f(0)$;
②若m+n<0,即m<-n,
所以f(m)<f(-n),m3<(-n)3,
又因为$f(x)=\frac{1}{2}-\frac{1}{{{2^x}+1}}$在R上是奇函数,
所以f(-n)=-f(n),f(m)+f(n)<0,m3+n3<0
所以$\frac{f(m)+f(n)}{{{m^3}+{n^3}}}>0$,
又因为f(0)=0,
所以$\frac{f(m)+f(n)}{{{m^3}+{n^3}}}>f(0)$.
综上所述:当m+n≠0时,$\frac{f(m)+f(n)}{{{m^3}+{n^3}}}>f(0)$.
点评 本题主要考查函数奇偶性和单调性的应用,结合分式函数的性质是解决本题的关键.考查学生的运算和推理能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6x+y-11=0 | B. | 6x-y-11=0 | C. | x-6y-11=0 | D. | x+6y+11=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
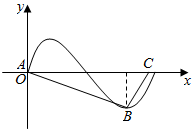 已知函数f(x)=sinωx(ω>0)的一段图象如图所示,△ABC的顶点A与坐标原点重合,B是f(x)的图象上一个最低点,C在x轴上,若内角A,B,C所对边长分别为a,b,c,且△ABC的面积满足S=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{12}$,将f(x)的图象向右平移一个单位得到g(x)的图象,则g(x) 的表达式为-cos($\frac{π}{2}$x).
已知函数f(x)=sinωx(ω>0)的一段图象如图所示,△ABC的顶点A与坐标原点重合,B是f(x)的图象上一个最低点,C在x轴上,若内角A,B,C所对边长分别为a,b,c,且△ABC的面积满足S=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{12}$,将f(x)的图象向右平移一个单位得到g(x)的图象,则g(x) 的表达式为-cos($\frac{π}{2}$x).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 15$\sqrt{3}$km | B. | 30km | C. | 15km | D. | 15$\sqrt{2}$km |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 直线a,b,c,若a∥b,b∥c,则a∥c,类推出:向量$\overrightarrow a$,$\overrightarrow b$,$\overrightarrow c$,若$\overrightarrow a$∥$\overrightarrow b$,$\overrightarrow b$∥$\overrightarrow c$,则$\overrightarrow a$∥$\overrightarrow c$ | |
| B. | 同一平面内,直线a,b,c,若a⊥c,b⊥c,则a∥b,类推出:空间中,直线a,b,c,若a⊥c,b⊥c,则a∥b | |
| C. | 实数a,b,若方程x2+ax+b=0有实数根,则a2≥4b,类推出:复数a,b,若方程x2+ax+b=0有实数根,则a2≥4b | |
| D. | 由向量加法的几何意义,可以类比得到复数加法的几何意义 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com