
| A. | (-∞,-2) | B. | (-∞,-2] | C. | (-∞,0) | D. | (-∞,0] |
分析 先把函数y=2${\;}^{{x}^{2}+4x+1}$分解为y=2t与t=x2+4x+1,因为y=2t单调递增,所以要求函数y=2${\;}^{{x}^{2}+4x+1}$的单调递减区间只需求函数t=x2+4x+1的单调减区间即可.
解答 解:令t=x2+4x+1,则函数y=2${\;}^{{x}^{2}+4x+1}$可看作由y=2t与t=x2+4x+1复合而成的.
由t=x2+4x+1=(x+2)2-3,得函数t=x2+4x+1的单调减区间是(-∞,-2),
又y=2t单调递增,所以函数y=2${\;}^{{x}^{2}+4x+1}$的单调递减区间是(-∞,-2).
故选:A.
点评 本题考查指数函数的单调性、二次函数的单调性以及复合函数单调性的判定方法,该类问题一要考虑函数定义域,二要遵循“同增异减”的规律.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$+1 | B. | $\frac{{1+\sqrt{3}}}{2}$ | C. | 2 | D. | $\frac{{1+\sqrt{5}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
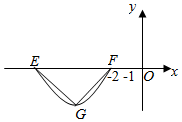 偶函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,其中△EFG是斜边为4的等腰直角三角形(E、F是函数图象与x轴的交点,点G在图象上),则f(1)的值为( )
偶函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,其中△EFG是斜边为4的等腰直角三角形(E、F是函数图象与x轴的交点,点G在图象上),则f(1)的值为( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4π}{3}$ | B. | $\frac{8π}{3}$ | C. | $\frac{16π}{3}$ | D. | $\frac{32π}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com