
分析 (1)根据f(x)在[-1,1]上单调递减且存在零点可得f(-1)f(1)≤0,从而解出a的范围;
(2)对b进行讨论,判断g(x)的单调性,分别求出f(x),g(x)在[1,4]上的值域,令g(x)的值域为f(x)的值域的子集列出不等式组得出b的范围.
解答 解:(1)∵f(x)=x2-4x+a+3的函数图象开口向上,对称轴为x=2,
∴f(x)在[-1,1]上是减函数,
∵函数y=f(x)在[-1,1]上存在零点,
∴f(-1)f(1)≤0,即a(8+a)≤0,
解得:-8≤a≤0.
(2)a=3时,f(x)=x2-4x+6,
∴f(x)在[1,2]上单调递减,在[2,4]上单调递增,
∴f(x)在[2,4]上的最小值为f(2)=2,最大值为f(4)=6.
即f(x)在[2,4]上的值域为[2,6].
设g(x)在[1,4]上的值域为M,
∵对任意的x1∈[1,4],总存在x2∈[1,4],使得g(x1)=f(x2),
∴M⊆[2,6].
当b=0时,g(x)=5,即M={5},符合题意,
当b>0时,g(x)=bx+5-2b在[1,4]上是增函数,
∴M=[5-b,5+2b],
∴$\left\{\begin{array}{l}{5-b≥2}\\{5+2b≤6}\\{b>0}\end{array}\right.$,解得0<b≤$\frac{1}{2}$.
当b<0时,g(x)=bx+5-2b在[1,4]上是减函数,
∴M=[5+2b,5-b],
∴$\left\{\begin{array}{l}{5+2b≥2}\\{5-b≤6}\\{b<0}\end{array}\right.$,解得-1≤b<0.
综上,b的取值范围是$[-1,\frac{1}{2}]$.
点评 本题考查了二次函数的单调性判断,值域计算,零点的存在性定理,分类讨论思想,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=lnx3 | B. | y=-x2 | C. | y=-$\frac{1}{x}$ | D. | y=x|x| |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(-$\frac{3}{4}$)<f(a2-a+1) | B. | f(-$\frac{3}{4}$)>f(a2-a+1) | C. | f(-$\frac{3}{4}$)≤f(a2-a+1) | D. | f(-$\frac{3}{4}$)≥f(a2-a+1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
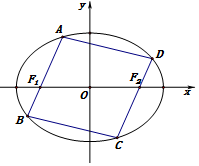 已知椭圆E的中心在原点,焦点F1、F2在x轴上,离心率为$\frac{1}{2}$,在椭圆E上有一动点A与F1、F2的距离之和为4,
已知椭圆E的中心在原点,焦点F1、F2在x轴上,离心率为$\frac{1}{2}$,在椭圆E上有一动点A与F1、F2的距离之和为4,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1)(3) | B. | (2)(4) | C. | (2)(3)(4) | D. | (1)(2)(3)(4) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | e2f(2)>e3f(3) | B. | e2f(2)<e3f(3) | C. | e2f(2)≥e3f(3) | D. | e2f(2)≤e3f(3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com