Question

2．正方形ABCD边长为2，AD中点为p，一个动点M从A出发沿着正方形的边移动依次到达B、C、D结束．（在这个过程中，M点走过的路程为x，以MP为边的正方形的面积为y．）
（1）找出x与y的函数关系式．
（2）关于x的方程y=k有两个不相等的实根，求k的取值范围．

Answer 1

分析 （1）通过对点M的位置进行讨论，并利用勾股定理即得结论；
（2）通过画出图象，数形结合即得结论．

解答 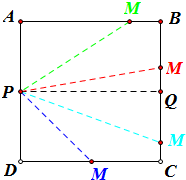解：（1）依题意，0≤x≤6，
如图，取BC的中点Q并连结PQ，
则|AP|=|PD|=|BQ|=|QC|=1，|PQ|=2，
下面对点M的位置进行讨论：
①当0≤x＜2时，点M位于线段AB上，
此时y=|MP|²=|AM|²+|AP|²=x²+1；
②当2≤x＜3时，点M位于线段BQ上，
此时y=|MP|²=|MQ|²+|PQ|²=（3-x）²+4=x²-6x+13；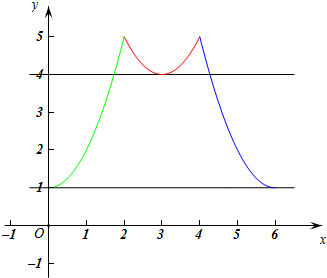
③当3≤x＜4时，点M位于线段QC上，
此时y=|MP|²=|MQ|²+|PQ|²=（x-3）²+4=x²-6x+13；
④当4≤x≤6时，点M位于线段CD上，
此时y=|MP|²=|MD|²+|PD|²=（6-x）²+1=x²-12x+37；
综上所述，y=$\left\{\begin{array}{l}{{x}^{2}+1，}&{0≤x＜2}\\{{x}^{2}-6x+13，}&{2≤x＜4}\\{{x}^{2}-12x+37，}&{4≤x≤6}\end{array}\right.$；
（2）由（1），画出分段函数y的图象如图，
∵关于x的方程y=k有两个不相等的实根，
∴直线y=k与（1）中函数图象有两个不同个交点，
∴1≤k＜4，
由图象可知，当k=5时，方程y=k也有两个不相等的实根．
即k的取值范围为：1≤k＜4或k=5．

点评 本题考查函数解析式，考查数形结合，注意解题方法的积累，属于中档题．