
分析 对于①,根据含有量词的命题的否定即可判断;对于②,先利用二倍角公式将f(x)化简,然后根据T=$\frac{2π}{|ω|}$求出a的值,再判断充分必要性;对于③,根据向量数量积的定义以及两向量夹角的取值范围进行判断;对于④,根据幂函数的性质分别判断四个函数在(0,+∞)上的单调性即可.
解答 解:对于①:全称命题的否定是存在性命题(也叫特称命题),所以命题“?x0∈R,x02+1>3x0”的否定是“?x∈R,x2+1≤3x”,故①正确;
对于②:由二倍角公式可知,f(x)=cos2ax-sin2ax=cos2ax,由T=$\frac{2π}{|2a|}=π$,得a=±1,因为“a=±1“是“a=1”的必要不充分条件,故②正确;
对于③:记$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为θ.若平面向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角是钝角,则$\overrightarrow{a}•\overrightarrow{b}$=$|\overrightarrow{a}||\overrightarrow{b}|cosθ$<0;若$\overrightarrow{a}•\overrightarrow{b}$<0,则cosθ<0,即$\overrightarrow{a}$与$\overrightarrow{b}$的夹角θ是钝角或平角(即180°).
所以“$\overrightarrow{a}•\overrightarrow{b}$<0”是“平面向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角是钝角”的必要不充分条件,故③不正确;
对于④:根据幂函数的性质,y=x-1在(0,+∞)上是减函数,y=${x^{\frac{1}{2}}}$,y=x2,y=x3其中在(0,+∞)上是增函数,故④正确.
故答案为:①②④
点评 本题主要考查了命题的真假判断,同时也考查了含有量词的命题的否定,三角函数,向量以及幂函数的性质等知识点,对学生要求较高,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2 | C. | $2\sqrt{2}$ | D. | 以上都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2-$\sqrt{2}$,1] | B. | (2-$\sqrt{2}$,2+$\sqrt{2}$] | C. | (-∞,2-$\sqrt{2}$)∪(2+$\sqrt{2}$,+∞) | D. | [-1,$\sqrt{2}$-2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
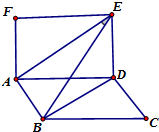 如图,矩形ADEF和矩形ABCD有公共边AD.
如图,矩形ADEF和矩形ABCD有公共边AD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
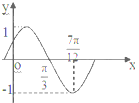 把函数y=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象向左平移$\frac{π}{3}$个单位得到y=f(x)的图象(如图),则2A-ω+φ=( )
把函数y=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象向左平移$\frac{π}{3}$个单位得到y=f(x)的图象(如图),则2A-ω+φ=( )| A. | $-\frac{π}{3}$ | B. | $\frac{π}{3}$ | C. | $-\frac{π}{6}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{1}{2}$] | B. | [$\frac{1}{2}$,+∞) | C. | (-2,$\frac{1}{2}$] | D. | [$\frac{1}{2}$,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com