

| 分组 | 频数 | 频率 | 频率/组距 |
| … | … | … | … |
| [180,185) | x | y | z |
| [185,190) | m | n | p |
| … | … | … | … |
分析 (1)由频率分布直方图得前5组的频率和第8组的频率,从而得到第6、7组的频率,进而得到样本中第6、7组的总人数为7人,再由x,m,2成等差数列,能求出结果,并补充完成频率分布直方图.
(2)由频率分布直方图,能求出求出平均数,众数,中位数.
(3)身高属于第六组的学生有4人,身高属于第八组的学生有2人,由此能求出至少有一名男生来自第六组的概率.
解答 解:(1)由频率分布直方图得前5组的频率是:
(0.008+0.016+0.04+0.04+0.06)×5=0.82,
第8组的频率是0.04,
∴第6、7组的频率是1-0.82-0.04=0.17,
∴样本中第6、7组的总人数为7人,
由已知得:x+m=7,①
∵x,m,2成等差数列,∴x=2m-2,②
由①②得:m=3,x=4,
∴y=0.08,n=0.06,p=0.012.
补充完成频率分布直方图如下图: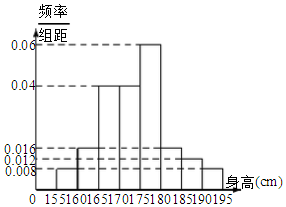
(2)由频率分布直方图得:
平均数为:157.5×0.008×5+162.5×0.016×5+167.5×0.04×5+172.5×0.04×5+177.5×0.06×5+182.5×0.016×5+187.5×0.012×5+192.5×0.008×5=174.1.
众数为:$\frac{175+180}{2}$=177.5.
∵前4组的频率为(0.008+0.016+0.04)×5=0.32,
∴中位数为:170+$\frac{0.5-0.32}{0.04×5}×5$=174.5.
(3)身高属于第六组的学生有0.016×5×50=4人,
身高属于第八组的学生有0.008×5×50=2人
从身高属于第六组和第八组的所有学生中随机抽取2名学生,
基本事件总数n=${C}_{6}^{2}$=15,
至少有一名男生来自第六组的概率p=1-$\frac{{C}_{2}^{2}}{{C}_{6}^{2}}$=$\frac{14}{15}$.
点评 本题考查频率分布直方图的画法,考查平均数,众数,中位数、概率的求法,是基础题,解题时要认真审题,注意频率分布直方图的性质的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | {-2,2} | B. | {-2,0,2} | C. | {-2,-1,2} | D. | {-2,-1,0,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD的底面ABCD是正方形,PD⊥平面ABCD.
如图,四棱锥P-ABCD的底面ABCD是正方形,PD⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | -$\frac{π}{3}$ | D. | -$\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com