
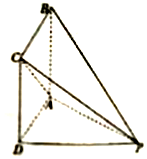
 如图,四棱锥P-ABCD的底面ABCD是正方形,PD⊥平面ABCD.
如图,四棱锥P-ABCD的底面ABCD是正方形,PD⊥平面ABCD.分析 (1)线线垂直转化为证明线面垂直,连接BD.PD⊥平面ABCD,可得PD⊥AC,BD⊥AC,可知AC⊥平面PBD,故得AC⊥PB;
(2)异面直线所成的角要转化为平面角,通过平移相交寻找.底面ABCD是正方形,AD∥BC,可得异面直线PB与AD所成角为∠PBC.在三角形PBC中求解∠PBC的余弦值即可.
解答 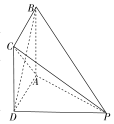 解:(1)证明:连接BD.
解:(1)证明:连接BD.
∵PD⊥平面ABCD,
∴PD⊥AC,
∵底面ABCD是正方形,
∴BD⊥AC,
又PD∩BD=D,
∴AC⊥平面PBD,
∵PB?平面PBD,
∴AC⊥PB.得证.
(2)在Rt△PDB中,$PB={3^2}+{(2\sqrt{2})^2}=\sqrt{17}$.
∵PD⊥平面ABCD,
∴PD⊥BC,又BC⊥CD,
∴BC⊥平面PCD,
∴BC⊥PC.
∵BC∥AD,
∴∠PBC即为异面直线PB与AD所成的角,
∴$cos∠PBC=\frac{BC}{PB}=\frac{{2\sqrt{17}}}{17}$.
故得异面直线PB与AD所成角的余弦值为$\frac{2\sqrt{17}}{17}$.
点评 本题考查两条垂直的证明和异面直线所成角的大小的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:选择题
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $?p:?x>2,{log_2}(x+\frac{4}{x})≤2$且¬p为真命题 | |
| B. | $?p:?x≤2,{log_2}(x+\frac{4}{x})>2$且¬p为真命题 | |
| C. | $?p:?x>2,{log_2}(x+\frac{4}{x})≤2$且¬p为假命题 | |
| D. | $?p:?x≤2,{log_2}(x+\frac{4}{x})>2$且¬p为假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M∩N=M | B. | M∪(∁UN)=U | C. | M∩(∁UN)=∅ | D. | M⊆∁UN |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{n}{2n+1}$ | B. | $\frac{n}{2n-1}$ | C. | $\frac{n}{2n-3}$ | D. | $\frac{n}{2n+3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

| 分组 | 频数 | 频率 | 频率/组距 |
| … | … | … | … |
| [180,185) | x | y | z |
| [185,190) | m | n | p |
| … | … | … | … |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com