Question

9．已知函数f（x）=|2x-1|+|x-a|．
（1）当a=2时，解不等式：f（x）≤x+3
（2）当x，y∈Z，则称点P（x，y）为平面上单调格点；若（2x，y）或（x，2y）为格点，则称点P（x，y）为半格点．设Q={（x，y）|$\left\{\begin{array}{l}{0≤x≤2}\\{0≤x≤3}\end{array}\right.$}，A={（x，y）|f（x）≤y≤3，a=2}．
①求从区域Ω中任取一点P，而该点落在区域A上的概率；
②求从区域Ω中的所有格点或半格点中任取一点P，而该点是区域A上的格点或半格点的概率．

Answer 1

分析 （1）分类讨论，解不等式即可；
（2）①记事件M=“从区域Ω中任取一点P，而该点落在区域A上”，则事件M符合几何概型；②记事件N=“从区域Ω中的所有格点或半格点中任取一点P，而该点是区域A上的格点或半格点”，则事件N符合古典概型．

解答 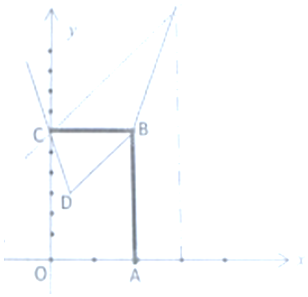解：（1）当a=2时，x≥2，f（x）≤x+3可化为3x-3≤x+3，∴x≤3，∴2≤x≤3；
$\frac{1}{2}＜$x＜2，f（x）≤x+3可化为x+1≤x+3恒成立；
x$≤\frac{1}{2}$，f（x）≤x+3可化为3-3x≤x+3，∴x≥0，∴0≤x≤$\frac{1}{2}$；
综上所述，不等式：f（x）≤x+3的解集为[0，3]；
（2）作出集合Ω及A所对应的区域（如图）：矩形OABC与△BCD，则：
①记事件M=“从区域Ω中任取一点P，而该点落在区域A上”，
则事件M符合几何概型，即P=$\frac{\frac{1}{2}•3•\frac{3}{2}}{2•3}$=$\frac{3}{8}$．
②记事件N=“从区域Ω中的所有格点或半格点中任取一点P，而该点是区域A上的格点或半格点”，
则事件N符合古典概型．
区域Ω中的格点个数：
格点个数：当横坐标分别为0，1，2时，纵坐标可以为0，1，2，3中的任一个，此时有3×4=12个；
半格点个数：当横坐标为$\frac{1}{2}，\frac{3}{2}$时，纵坐标为整数0，1，2，3，此时有2×4=8个，
当纵坐标为$\frac{1}{2}，\frac{3}{2}，\frac{5}{2}$时，横坐标为整数0，1，2，此时共有9个，即区域Ω中的格点或半格点个数有29个，而区域A中的格点或半格点有（0，3），（1，3），（2，3），（1，2），（$\frac{1}{2}，2$），（$\frac{1}{2}，3）$，（$\frac{3}{2}$，3）共7个，
∴P=$\frac{7}{29}$．

点评 本题考查解不等式，考查概率的计算，考查学生分析解决问题的能力，属于中档题．