Question

4．过△ABC的重心G的直线l分别与边AB、AC交于F、E两点，设$\overrightarrow{AE}$=x$\overrightarrow{AC}$，$\overrightarrow{AF}$=y$\overrightarrow{AB}$（x＞0，y＞0），则x+y的最小值为$\frac{4}{3}$．

Answer 1

分析 可画出图形，由条件可得到$\overrightarrow{AC}=\frac{1}{x}\overrightarrow{AE}，\overrightarrow{AB}=\frac{1}{y}\overrightarrow{AF}$，且$\overrightarrow{AG}=\frac{1}{3}（\overrightarrow{AB}+\overrightarrow{AC}）$，进而得出$\overrightarrow{AG}=\frac{1}{3x}\overrightarrow{AE}+\frac{1}{3y}\overrightarrow{AF}$，从而得出$\frac{1}{3x}+\frac{1}{3y}=1$，从而$x+y=（x+y）（\frac{1}{3x}+\frac{1}{3y}）$，然后根据基本不等式即可求出x+y的最小值．

解答 解：如图，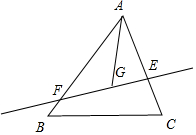
根据条件：$\overrightarrow{AC}=\frac{1}{x}\overrightarrow{AE}，\overrightarrow{AB}=\frac{1}{y}\overrightarrow{AF}$；
又$\overrightarrow{AG}=\frac{1}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}$；
∴$\overrightarrow{AG}=\frac{1}{3x}\overrightarrow{AE}+\frac{1}{3y}\overrightarrow{AF}$；
又F，G，E三点共线；
∴$\frac{1}{3x}+\frac{1}{3y}=1$；
∵x＞0，y＞0；
∴$x+y=（x+y）（\frac{1}{3x}+\frac{1}{3y}）$=$\frac{1}{3}+\frac{x}{3y}+\frac{y}{3x}+\frac{1}{3}$$≥\frac{2}{3}+2\sqrt{\frac{x}{3y}•\frac{y}{3x}}=\frac{4}{3}$；
x+y的最小值为$\frac{4}{3}$．
故答案为：$\frac{4}{3}$．

点评 考查三角形重心的概念及性质，向量数乘的几何意义，向量加法的平行四边形法则，以及三点共线的充要条件，基本不等式的应用．