练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    16．设数列{an}是集合{3s+3t|0≤s＜t，且s，t∈Z}中所有的数从小到大排列成的数列，即a1=4，a2=10，a3=12，a4=28，a5=30，a6=36，…，将数列{an}中各项按照上小下大，左小右大的原则排成如图等腰直角三角形数表，a200的值为（　　）
    A．39+319B．310+319C．319+320D．310+320

    分析 如果用（t，s）表示3s+3t，则4=（0，1）=30+31，10=（0，2）=30+32，12=（1，2）=31+32，…．利用归纳推理即可得出．

    解答 解：如果用（t，s）表示3s+3t，
    则4=（0，1）=30+31，
    10=（0，2）=30+32，
    12=（1，2）=31+32，
    28=（0，3）=30+33，
    30=（1，3）=31+33，
    36=（2，3）=32+33，…．
    利用归纳推理即可得：t+1表示从左到右的个数代表行数，s表示行数，
    当t=19时，最后一项为1+2+…+19=190，
    当t=20时，最后一项为1+2+…+20=210，
    第191为第20行第一个数，210-190=t+1，∴t=19．
    ∴a200一定在第20行，则a200=（19，20），则a200=319+320，
    故选：C．

    点评 本题考查了指数幂的运算性质、归纳法，考查了推理能力与计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    6．用秦九韵算法计算多项式f（x）=5x5+4x4+3x3+2x2+x+1，当x=5时，乘法运算的次数为5；加法运算的次数为5．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．下面各组函数中是同一函数的是（　　）
    （1）$y=\sqrt{-2{x^3}}与y=x\sqrt{-2x}$
    （2）$y={（\sqrt{x}）^2}$与y=|x|
    （3）$y=\sqrt{x+1}•\sqrt{x-1}与y=\sqrt{（x+1）（x-1）}$
    （4）f（x）=x2-2x-1与g（t）=t2-2t-1．
    A．（1）（3）（4）B．（1）（2）（3）C．（3）（4）D．（4）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．过△ABC的重心G的直线l分别与边AB、AC交于F、E两点，设$\overrightarrow{AE}$=x$\overrightarrow{AC}$，$\overrightarrow{AF}$=y$\overrightarrow{AB}$（x＞0，y＞0），则x+y的最小值为$\frac{4}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．已知焦点在x轴上的椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{3}$=1，其离心率为$\frac{1}{2}$，过椭圆左焦点F1与上顶点B的直线为l0．
    （1）求椭圆的方程及直线l0的方程；
    （2）直线l：y=kx（k≠0）与椭圆C交于M，N两点，点P是椭圆上异于M，N的一点．
    ①求证：当直线PM，PN存在斜率时，两直线的斜率之积为定值，即kPM•kPN为定值；
    ②当直线l与点P满足什么条件时，△PMN有最大面积？并求此最大面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．已知{an}为等差数列，Sn为其前n项和，若a1=6，a3+a5=0，则S6=（　　）
    A．6B．5C．3D．0

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．已知x，y满足约束条件$\left\{\begin{array}{l}x-y-2≤0\\ 5x-3y-12≥0\\ y≤3\end{array}\right.$，当目标函数z=ax+by（a＞0，b＞0）在该约束条件下取得最小值1时，（a+1）2+（b-1）2的最小值为（　　）
    A．$\frac{1}{10}$B．$\frac{{\sqrt{10}}}{10}$C．$\frac{{3\sqrt{10}}}{10}$D．$\frac{9}{10}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

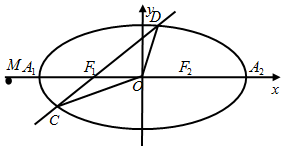    5．（文科）如图，已知椭圆的中心在坐标原点，焦点F1，F2，在x轴上，长轴A1A2的长为4，x轴上一点M（${-\frac{a^2}{c}，0}$），$|{\overrightarrow{M{A_1}}}|$=$2|{\overrightarrow{{A_1}{F_1}}}|$．
    （1）求椭圆的方程；
    （2）过左焦点F1且斜率为1的直线l与椭圆相交于C、D两点，求△OCD的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．已知f（x+1）=2x-1，则f（x）=2x-3．

    查看答案和解析>>

    同步练习册答案