
| A�� | �۽������� | B�� | ��������� | C�� | ֱ�������� | D�� | ��ȷ�� |
���� �ɻ���ͼ�Σ����������ó�$\overrightarrow{AM}=\frac{1}{2}��\overrightarrow{AB}+\overrightarrow{AC}��$���Ӷ��ɽ������������������$\overrightarrow{AM}•\overrightarrow{AD}=0$�������ó�$\overrightarrow{AM}��\overrightarrow{AD}$���Ӷ��жϳ���AMD����״��
��� 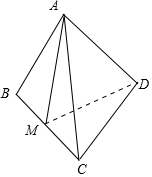 �⣺��ͼ��
�⣺��ͼ��
����������
$\overrightarrow{AM}•\overrightarrow{AD}=\frac{1}{2}��\overrightarrow{AB}+\overrightarrow{AC}��•\overrightarrow{AD}$
=$\frac{1}{2}��\overrightarrow{AB}•\overrightarrow{AD}+\overrightarrow{AC}•\overrightarrow{AD}��$
=0��
��$\overrightarrow{AM}��\overrightarrow{AD}$��
���AMDΪֱ�������Σ�
��ѡC��
���� ���������ӷ���ƽ���ı��η����Լ����������������㣬������ֱ�ij�Ҫ������


 ��ǰ����ϵ�д�
��ǰ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {2} | B�� | {1��2��2��4} | C�� | ∅ | D�� | {1��2��4} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 6 | B�� | 5 | C�� | 3 | D�� | 0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{10}$ | B�� | $\frac{{\sqrt{10}}}{10}$ | C�� | $\frac{{3\sqrt{10}}}{10}$ | D�� | $\frac{9}{10}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
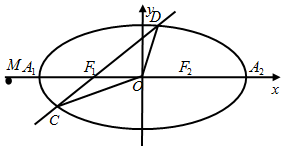 ���Ŀƣ���ͼ����֪��Բ������������ԭ�㣬����F1��F2����x���ϣ�����A1A2�ij�Ϊ4��x����һ��M��${-\frac{a^2}{c}��0}$����$|{\overrightarrow{M{A_1}}}|$=$2|{\overrightarrow{{A_1}{F_1}}}|$��
���Ŀƣ���ͼ����֪��Բ������������ԭ�㣬����F1��F2����x���ϣ�����A1A2�ij�Ϊ4��x����һ��M��${-\frac{a^2}{c}��0}$����$|{\overrightarrow{M{A_1}}}|$=$2|{\overrightarrow{{A_1}{F_1}}}|$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com