
����Ŀ�������������ƹ�������ߴ���ȫ���������飬Ѹ��Ӯ�ù�������ߵ�������Ȼ����ͬʱҲ��¶��������ͣ�š�����ȷ�������⣬Ϊ���˽�ڶԹ���������̬�ȣ��ᳫ���ᳫ����ij����С������ضԲ�ͬ�����50�˽��е��飬����������������±���

���ң�������![]() ��
��![]() �����г֡��ᳫ��̬�ȵ������ֱ�Ϊ5��3���ִ�������������������ȡ2���������.
�����г֡��ᳫ��̬�ȵ������ֱ�Ϊ5��3���ִ�������������������ȡ2���������.
������������![]() �б��鵽��2�˶��֡��ᳫ��̬�ȵĸ��ʣ�
�б��鵽��2�˶��֡��ᳫ��̬�ȵĸ��ʣ�
������������![]() �б��鵽��2������1�˳֡��ᳫ��̬�ȵĸ���.
�б��鵽��2������1�˳֡��ᳫ��̬�ȵĸ���.
���𰸡���1��![]() ����2��
����2��![]() .
.
�������������������1��������[20��25���й���6�ˣ����г����ᳫ��̬�ȵ�����Ϊ5�����г����ˣ������¼�����n=15�����鵽��2�˶������ᳫ��̬�Ȱ����Ļ����¼�����m=10���ɴ������������[20��25���б��鵽��2�˶������ᳫ��̬�ȵĸ��ʣ���2��������[40��45���й���5�ˣ����г����ᳫ��̬�ȵ�����Ϊ3�����г����ˣ������¼�����n��=10��������[40��45���б��鵽��2������1�˳����ᳫ��̬�Ȱ����Ļ����¼�����m��=9���ɴ������������[40��45���б��鵽��2������1�˳����ᳫ��̬�ȵĸ��ʣ�
������
��1������![]() �е�6�˳֡��ᳫ��̬�ȵ�Ϊ
�е�6�˳֡��ᳫ��̬�ȵ�Ϊ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ���֡����ᳫ��̬�ȵ�Ϊ
���֡����ᳫ��̬�ȵ�Ϊ![]() .
.
�ܵĻ����¼��У�![]() ������
������![]() ������
������![]() ������
������![]() ������
������![]() ������
������![]() ������
������![]() ������
������![]() ������
������![]() ������
������![]() ������
������![]() ������
������![]() ������
������![]() ������
������![]() ������
������![]() ��.��15�����������˶��֡��ᳫ��̬�ȵ���10����
��.��15�����������˶��֡��ᳫ��̬�ȵ���10����
����P=![]() =
=![]()
��2������![]() �е�5�˳֡��ᳫ��̬�ȵ�Ϊ
�е�5�˳֡��ᳫ��̬�ȵ�Ϊ![]() ��
�� ![]() ��
�� ![]() ���֡����ᳫ��̬�ȵ�Ϊ
���֡����ᳫ��̬�ȵ�Ϊ![]() ��
�� ![]() .
.
�ܵĻ����¼���(![]() )��(
)��(![]() )��(
)��(![]() )��(
)��(![]() )��(
)��(![]() )��(
)��(![]() )��(
)��(![]() )��(
)��(![]() )��(
)��(![]() )��(
)��(![]() )����10�����������˶��֡����ᳫ��̬�ȵ�ֻ��(
)����10�����������˶��֡����ᳫ��̬�ȵ�ֻ��(![]() )һ�֣�����P=
)һ�֣�����P=![]() =
=![]()
�����͡������
��������
22
����Ŀ����ƽ��ֱ������ϵ��ԭ��Ϊ���㣬 ![]() ��������Ϊ���Ὠ��������ϵ����֪Բ
��������Ϊ���Ὠ��������ϵ����֪Բ![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() ��ֱ��
��ֱ��![]() �IJ�������Ϊ
�IJ�������Ϊ![]() ��
��![]() ����������
����������![]() ��
��![]() ����
����![]() ����.
����.
������Բ![]() ��ֱ�����귽����
��ֱ�����귽����
������![]() ����
����![]() ��ֵ.
��ֵ.

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x2��y2��2(t��3)x��2(1��4t2)y��16t4��9��0(t��R)��ͼ����Բ��
(1)��t��ȡֵ��Χ��
(2)��Բ�����ȡ���ֵʱt��ֵ��
(3)����P(3,4t2)��������Բ�ڣ���t��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼC,D����ABΪֱ����Բ�ϵ����㣬![]() ,F��AB�ϵ�һ�㣬��
,F��AB�ϵ�һ�㣬��![]() ,��Բ��AB����ʹ��C��ƽ��ABD����ӰE��BD�ϣ���֪
,��Բ��AB����ʹ��C��ƽ��ABD����ӰE��BD�ϣ���֪![]()

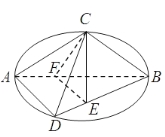
��1����֤��AD![]() ƽ��BCE
ƽ��BCE
��2����֤��AD//ƽ��CEF��
��3��������A-CFD�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ�����ⳤΪ2��������![]() �У�
�У� ![]() �ֱ�Ϊ
�ֱ�Ϊ![]() ��
��![]() ���е�.
���е�.
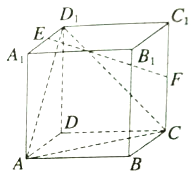
(1)��֤�� ![]() ƽ��
ƽ��![]() ��
��
(2)����![]() ���Ƿ����һ��
���Ƿ����һ��![]() ��ʹ�ö����
��ʹ�ö����![]() �Ĵ�СΪ
�Ĵ�СΪ![]() �������ڣ����
�������ڣ����![]() �ij����������ڣ���˵������.
�ij����������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����֪![]() ���溯��������m��ֵ��
���溯��������m��ֵ��
��2����������![]() ��ͼ������ͼ��ش�kΪ��ֵʱ������
��ͼ������ͼ��ش�kΪ��ֵʱ������![]() �⣿��һ�⣿�����⣿
�⣿��һ�⣿�����⣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�IJ���ʽ|x��3|+|x��m|��2m�Ľ⼯ΪR�� ������m�����ֵ��
������֪a��0��b��0��c��0����a+b+c=m����4a2+9b2+c2����Сֵ����ʱa��b��c��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() �ǹ��Ϊ0�ĵȲ����У�
�ǹ��Ϊ0�ĵȲ����У� ![]() ��
��![]() �ɵȱ����У�
�ɵȱ����У�
(1)������{an}��ͨ�ʽ��
(2)��![]() ��������
��������![]() ��ǰn���
��ǰn���![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��R����f��x��=��x+ ![]() ��ex�����䣨0��1����ֻ��һ����ֵ�㣬��a��ȡֵ��ΧΪ�� ��
��ex�����䣨0��1����ֻ��һ����ֵ�㣬��a��ȡֵ��ΧΪ�� ��
A.a��0
B.a��1
C.a��1
D.a��0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ![]() �У���
�У���![]() ��ֱ��
��ֱ��![]() ����Բ
����Բ![]() �İ뾶Ϊ1�� Բ����
�İ뾶Ϊ1�� Բ����![]() ��.
��.

��1����Բ��![]() Ҳ��ֱ��
Ҳ��ֱ��![]() �ϣ�����
�ϣ�����![]() ��Բ
��Բ![]() �����ߣ������߷��̣�
�����ߣ������߷��̣�
��2����Բ![]() �ϴ��ڵ�
�ϴ��ڵ�![]() ��ʹ
��ʹ![]() ����Բ��
����Բ��![]() �ĺ�����
�ĺ�����![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com